學生在學習整數、分數、小數的加、減法時，都會碰到比較型問題；此類型的問題一直困擾著部份學生，無法真正了解的學生就使用關鍵字解答問題。本文希望老師透過學生的親身經驗、語意轉換、圖形表徵，以及概念推廣、運算結構，讓學生真正了解比較型的意義，以培養學生帶得走的能力，以及學習數學的感覺。

 前言

李源順（2005）針對台北市、新北市和台中市國小各隨機取樣兩班三年級390名學生進行施測，發現學生碰到「比多用加」的比較型問題的答對率大約六成，對於「比少用加」的問題答對率大約三成七，如表1所示。作者發現比較型問題一直困擾著部分學生，但是它在整數加、減法時已經出現，到了分數、小數的加、減法時還是一再出現；因此作者想藉由有數學感的教學，說明如何讓學生學得有感覺，希望學生在某一個時間點真正了解以後，不管是整數、分數、小數的加、減法比較型問題，都能順利作答，培養學生帶得走的能力。

表1.比較型問題的答對率

 比較型問題

部分學生之所以對比較型問題產生困擾，主要有兩個原因：學生生活經驗的問題，以及數學概念的問題（李源順，2018）。

一、生活經驗與數學語意

比較型問題的生活語意有兩種，一種是直接說我比較多或者我多、你比較少或者你少，另一種是說我比你多，或者你比我少。對剛進入小學的學童而言，假如他的生活經驗比較少，他可能很少碰到兩個人在做比較的情境，例如，你吃的糖果和我吃的糖果誰吃得比較多、比較少的問題，因此可能不懂什麼叫做「比較多」或者「比較少」的生活語意。即使曾經有比較的生活經驗，大部分的學童也會直接、簡要地說「我比較多」或者「我多」、「你比較少」或者「你少」，在生活上比較少大費周章的說「我比你多」，或者「你比我少」。同時這兩種語意中「我」和「多」連在一起，但意義卻不相同；「我多」是「我比較多」，「你比我多」反而是「你比較多」，因此對部份學生會產生語意上的混淆。此外在同一個數學問題的文字表達上它有許多相同的語意，以「小明有5顆糖果，小英有3顆糖果」的脈絡為例，下表2的用語是完全相同的，也就是可以看成小明=5顆，小英=3顆。

表2.生活上與數學上相等的比較型用語

假如學生能了解上面的用語是相同的，相信對日後的比較型問題，困難會少很多。

二、數學概念--概念推廣與運算結構

在數學上，加法和減法的啟蒙概念就是合與分，也就是改變型或者合併型問題。以整數為例，「我有3顆糖果，我再得到2顆糖果，現在有幾顆糖果？」是把3顆和2顆糖果合起來是幾顆，它的算式是3+2=( 5 )；「我有5顆糖果，送出去3顆糖果，現在有幾顆糖果？」是把5顆分成3顆和幾顆，它的算式是5-3=( 2 )。它的圖形表徵分別如下圖1。


圖1.加法和減法改變型的啟蒙表徵圖

比較型問題是加法和減法的概念推廣。例如「小明有5顆糖果，小英有3顆糖果，小明比小英多幾顆糖果？」或者「小英比小明少幾顆糖果？」的問題，它的算式也是5-3=( 2 )，但是作者曾經在教學現場聽到學生說「小明怎麼可以拿走小英的糖果？」，也就是說，不可以把從小明的糖果減去小英的糖果。從語意轉換的角度，這個問題要用減法，必須說成「小明的5顆拿走自己和小英一樣多的3顆，剩下的2顆就是小明比小英多的2顆」；或者，剩下的2顆就是小英比小明少的2顆。語意轉換是培養小學生邏輯推理能力非常重要的過程，因此老師要設法讓學生能說清楚。此外，它的圖形表徵也和上面的不同，如圖2，它之所以要畫一對一的線，用意在說明把小明的5顆拿走自己和小英一樣多的3顆。


圖2.差未知的比較型問題之圖形表徵

在比較型的問題上，我們也可以運用運算結構來提升學生的語意轉換、邏輯推理能力，例如表3。

表3.相同比較型問題，但不同運算結構的問題


表3所示的第二、三個問題，其圖形表徵如圖3和圖4。老師要注意的地方是圖形的畫法，完全按照題目的順序去表徵它。同時它的解釋方式也需要做語意轉換：「小明有5顆糖果，小明比小英多2顆」的意思是「5顆比幾顆多2顆」、「把5顆扣掉多的2顆，就是幾顆」；「小英有3顆糖果，小明比小英多2顆糖果」語意可轉換為「幾顆比3顆多2顆」、「3顆加上多的2顆，就是幾顆」。


圖3.減數未知的比較型問題(一對一的線可以不畫)


圖4.被減數未知的比較型問題(一對一的線可以不畫)

在數學概念發展上，概念推廣和運算結構非常重要，例如乘法是加法、除法是減法、指數是乘法的概念推廣；分數、小數是整數的概念推廣。無論整數、分數、小數的加減法或者乘除法都有運算結構的問題。一旦學生發現概念推廣和運算結構的特性，對他而言，很多的數學問題變得非常容易，而且了解如何學習數學，變得更有數學感。

 教學過程

一、啟蒙教學

由於比較型問題的基本語意了解，與學生的生活經驗，同時與量的多寡、數的大小有關，因此老師在剛開始教學時，先確認數量的大小，再了解學生對「多、少」的生活語意是否了解，如表4。建議老師要留意低成就學生的回答，因為低成就學生的生活經驗比較差，詞句比較少，假如老師留意這些學童的學習，讓他從具體情境、較小的數量中會意，將有助於比較型問題的學習。老師可以請低成就學生回答或者每位學生寫下來，老師再個別檢查或者兩人一組互相檢查。必要時，老師可以將表2的內容寫出來，讓低成就學生說出來，以了解在「此一問題脈絡」下，它們的意義都是相同的。

表4.準備活動的教學過程 註：在教學過程中，有老師覺得低成就學生可能無法在老師說你，學生回答我之間進行轉換。作者認為這是生活中很基本的語言轉換，低成就學生一定要會。因此老師在教學時要多加留意。假如老師不想觸及此問題，可以改用老師和該生的名字來對話，例如老師有3顆，佳伶有5顆，是老師比較多或是佳伶比較多？老師在教學過程中，使用學生或者學生的名字，才能讓學生從親身的經驗中了解比較的意義。

表5的教學活動主要是讓學生發現比較型問題和上面改變型的圖形表徵不同，但算式相同；同時讓高成就學生能夠先進行語意轉換（換句話說）。

表5.教學活動


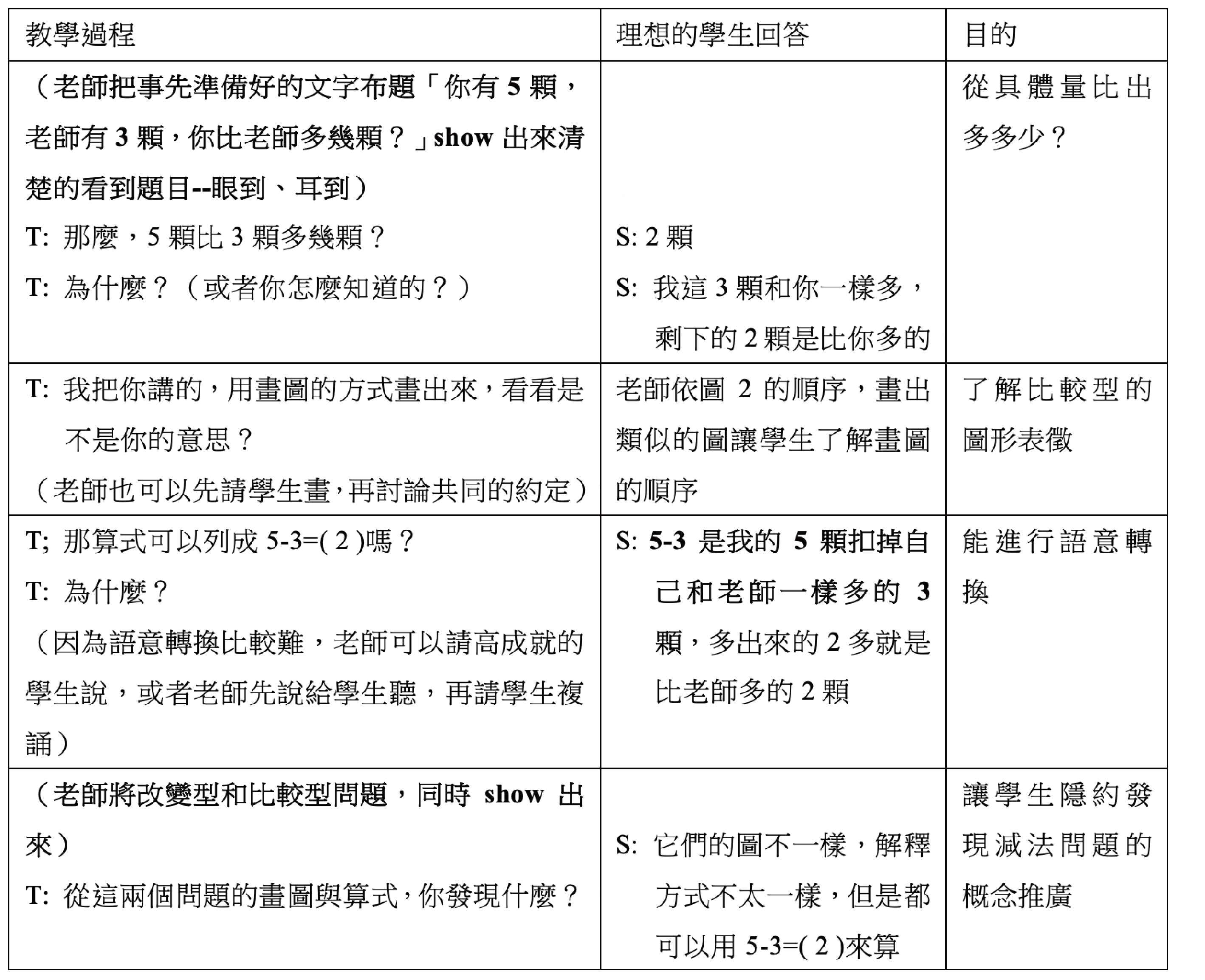
等到學生能了解上述的內容之後，老師可以在時間允許且學生能夠學習的情形下，設法將表2的多重語意讓學生說出來（將小明改成學生，小英改成老師），讓學生發現這些意思，在「你有5顆，老師有3顆」的前提下都是相同的。

老師再將學生融入其中的問題轉換為與自己無關的兩個人（例如小明和小英）、不同數字的問題，並了解是否有更多的學生能夠畫出它的圖形表徵、能夠進行語意轉換。若學生不懂，必須再回到學生自身的問題，設法讓學生發現，兩者的意義相同的。限於篇幅，教學活動的詳案不在本文羅列，請老師自行想像。

之後老師可以視教學時間或者在教科書有出現運算結構的情形下，將三種運算結構的問題，讓學生學習畫圖表徵、語意轉換，以比較、了解、發現其中的異同，擴展學生的學習經驗。
 

二、更大整數、分數、小數的加減法問題

當學生學習比較大的整數、分數、小數時，畫圖表徵會轉成線段圖來了解；當學生不了解時，老師可以使用類似的圖形表徵、換單位、簡化的方法，讓學生發現不管數字大小、分數、小數，它們的意義完全相同，如6。其中畫圖表徵有時候會畫成一條線，上、下分別代表不同的人（例如小數的畫法）；對不同的數字，換單位學生比較難懂，簡化數字則有時候情境比較不合理；但它們都是相同運算結構，同時一再重覆出現。因此，一旦低成就學生發現到其中的異同，相信所有比較型的問題會變得非常容易。

表6.數字大、分數、小數與較小問題的比較

 結語

因為比較型問題在不同位數的整數、分數、小數加減法一再重覆出現，只是它的數字、情境有變化，但是內容結構（包括運算結構、語句的變化）完全相同；同時，部分學生對比較型問題時常不了解題意而使用關鍵字來解答。假如老師的教學能讓學生發現：上面所談的語句完全相同，畫圖順序和題目順序相同，以及題目的運算結構變化和概念推廣的重要，相信比較型問題不再是困擾的問題，同時學生也能夠將上面的概念推廣到相類似的問題上。老師的教、學生的學會更有數學感。