
文/張惟淳
前言
「貓是液體」,這句話對有養貓的人而言一定不陌生,意思是貓咪絕佳的柔軟性讓牠的身體幾乎可以像液體一般塞滿各種容器,用網路搜尋可以找到許多的可愛圖片。
試想看看,我們有辦法在紙上畫出一隻貓,將牠剪成幾塊,然後塞進一個正方形裡嗎?答案是可以的!
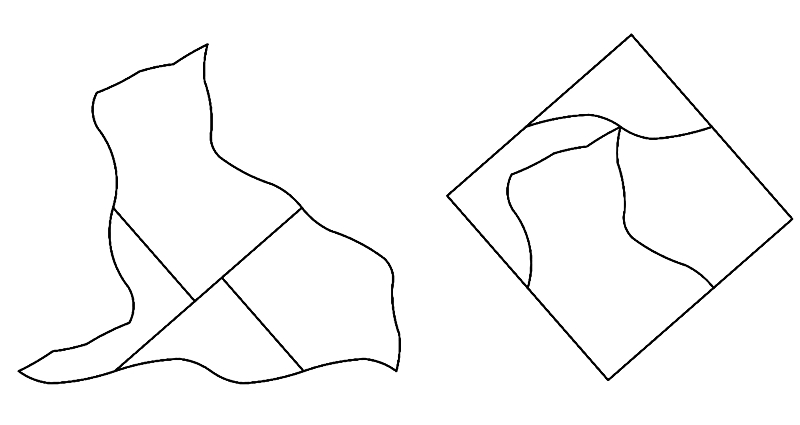
圖1. 貓咪變身為正方形
看的出來怎麼組裝的嗎?將左圖貓咪的「前腳」順時針旋轉 蓋到臉上,接著將「屁股」逆時針旋轉 貼住後腦勺,最後將下面的「肚子」向上平移到耳朵上面就完成了!雖然可憐的貓咪被分成了四塊,但牠真的剛好能夠重新組合成一個正方形。
本文的主旨即是在探討如何設計出一個這麼特殊的圖形,又如何將貓咪剪開重新拼成正方形,甚至拼成五邊形、六邊形以及不規則的幾何圖案,最後還可以無限地鋪滿整個平面。
為了瞭解這隻貓咪是怎麼畫的,我們要先準備四個預備知識:
預備知識一:裁縫師問題
這裡請您先思考一個問題:如何將一個正三角形切成幾片,重新組合成一個正方形呢?
這個問題是由美國數學家──亨利.杜德尼(Henry Dudeney)所提出的,又稱為裁縫師問題(haberdasher’s Problem)。其解法如下:
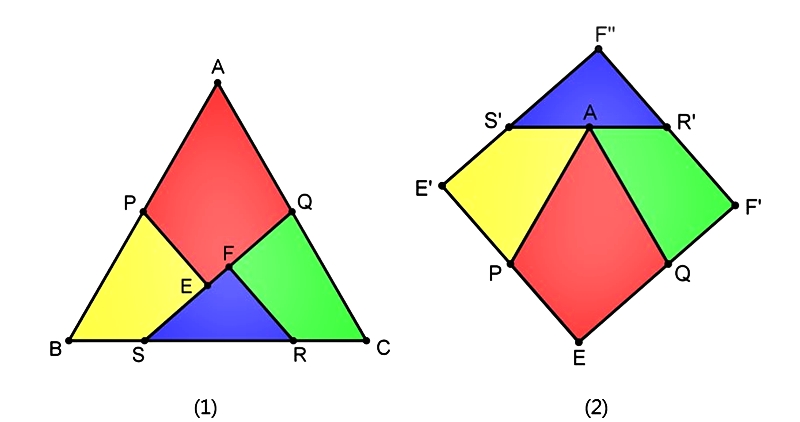
圖2. 裁縫師問題之解法
-
圖2(1),令正三角形ABC的邊長為2,取AB及AC邊上的中點P、Q。
-
自Q點作一長度為∜3的線段交BC於S。(註1)
-
作PE⊥QS於E。
-
在QS上取一點F使得SE=QF。
-
以F為垂足,作FR⊥QS於F,交BC於R。
沿線切開組成圖2(2),完畢。
裁縫師問題的切痕有許多不同的等價作法,以上僅列出其中一種。這個作法也可以用尺規作圖完成。
這種將圖形切開後再組裝為新圖形的方法,在數學上稱為「幾何解剖」(Geometric Dissection),是計算幾何學(Computational Geometry)下的一個分支。筆者相當中意這個命名法,所謂「解剖」泛指研究、拆解並分析生物器官的學問。這種問題不也像是讓三角形、正方形像是有了生命一樣,可以去分析它們的構造嗎?
另外,如果我們將P、Q、R、S這四點中的其中三點固定,就可以像樞紐一樣旋轉,這種每塊拼圖都可以一塊一塊旋轉的構造,又稱為樞紐解剖(Hinged Dissection)。見下頁圖:
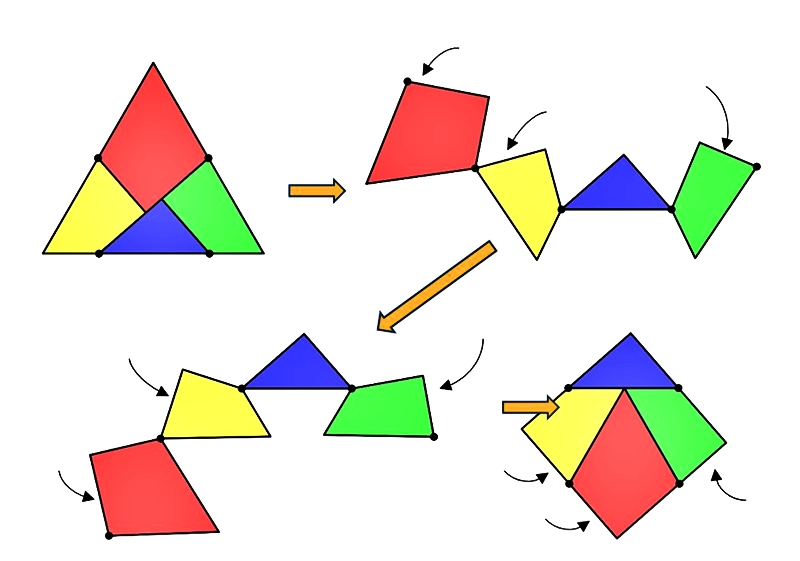
圖3. 樞紐解剖示例
看過上面的裁縫師問題的解答後,您可以思考看看,要「如何想到」這樣的解法呢?
預備知識二:鑲嵌
「鑲嵌」(tessellation),或是「密鋪」(tiling)指的是用同樣的圖形,不斷重複、不相交疊且毫無空隙地舖滿整個平面。在許多的美術、建築以及科技的設計中都可以見到它的蹤跡。僅重複使用一種正多邊形所形成的鑲嵌,稱為正鑲嵌(regular tessellation / regular tiling)。正鑲嵌只有三種:正三角形、正方形以及正六邊形,理由是只有這三個正多邊形的內角是 的因數。
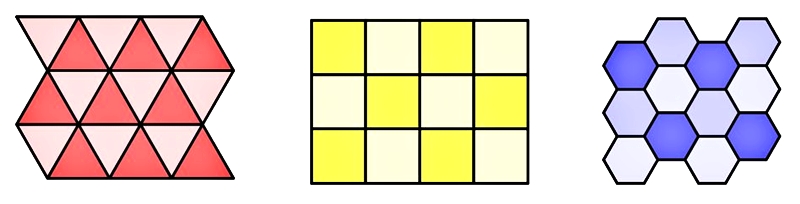
圖4. 三種正鑲嵌
筆者在這裡邊追加一個定義:使用同樣的圖形鋪滿一個定寬,但長度無限大的長方形時,這種圖形筆者稱之為「鑲嵌帶」。以正鑲嵌為例,可以發現正三角形和正方形的鑲嵌其實是可以看成數條鑲嵌帶所形成,所以可以讓每條鑲嵌帶進行錯動(錯位),但依然可以舖滿整個平面。
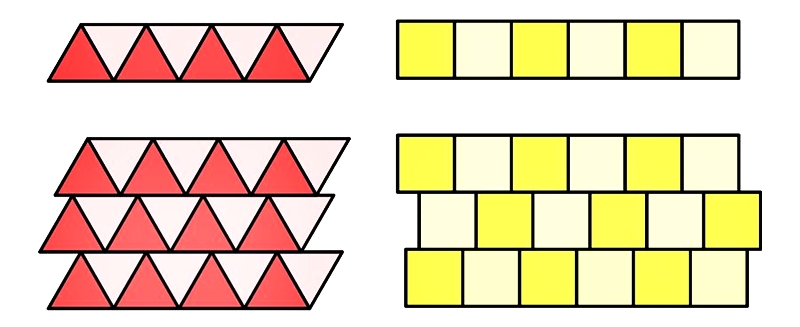
圖5. 鑲嵌帶
至於正鑲嵌和幾何解剖有什麼關聯性呢?關鍵在於鑲嵌帶的疊合。以裁縫師問題為例,正三角形和正方形恰好都是正鑲嵌的一種,我們就取同樣面積的正三角形和正方形組出鑲嵌帶,並且疊合,如下:
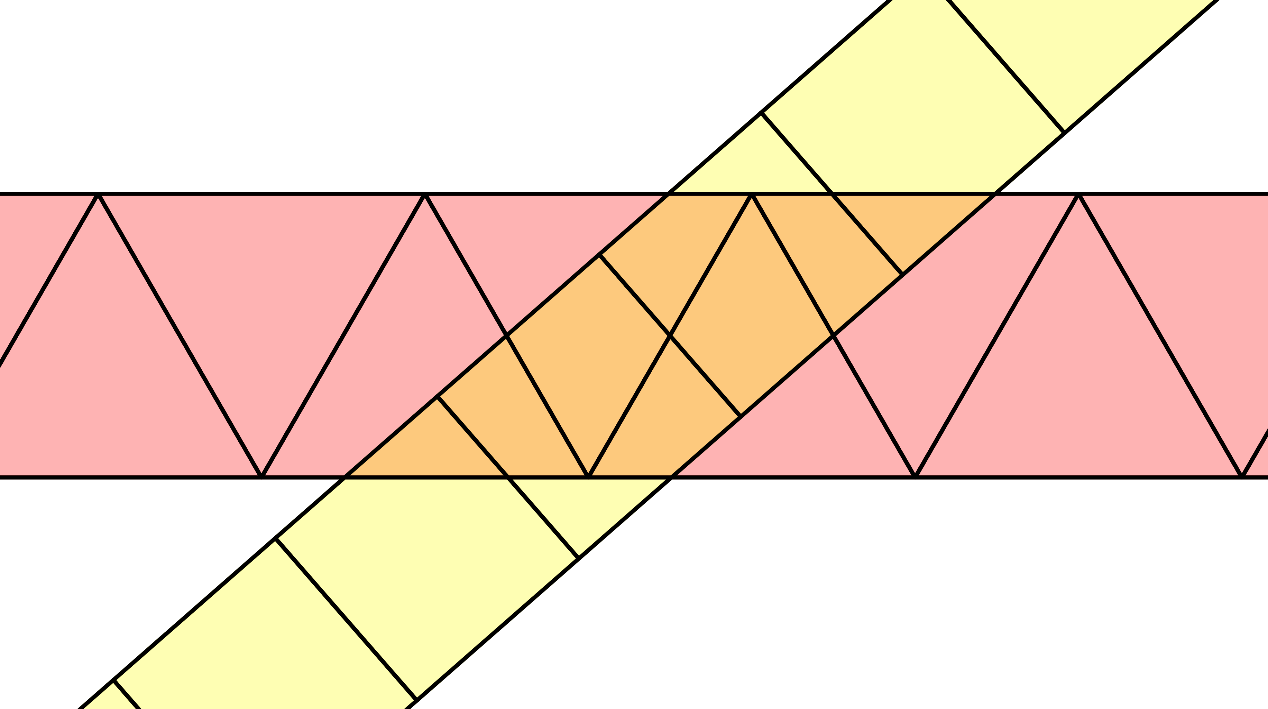
圖6. 鑲嵌帶解裁縫師問題
仔細觀察交疊處的正方形,恰好被切成了四塊。您發現了嗎?原來只要將兩條鑲嵌帶「適度地」疊合,就可以找出裁縫師問題的解法!這邊請您暫停閱讀,拿杯茶或者是咖啡,稍微思考一下。
不知道您是否會想提問以下這幾個問題:
-
什麼叫「適度地」疊合?
-
非正多邊形的鑲嵌都可以做到嗎?
-
無法形成鑲嵌的圖形(例如正五邊形),也可以藉由鑲嵌轉化為解剖嗎?
由於這並非本文的主旨,筆者不在這多進行說明,您可以在參考資料[6]的網站裡面找到非常豐富的結果。我們這裡先繼續延伸鑲嵌帶的結果。
將圖6.的正三角形和正方形的鑲嵌帶不斷重複,形成下圖:
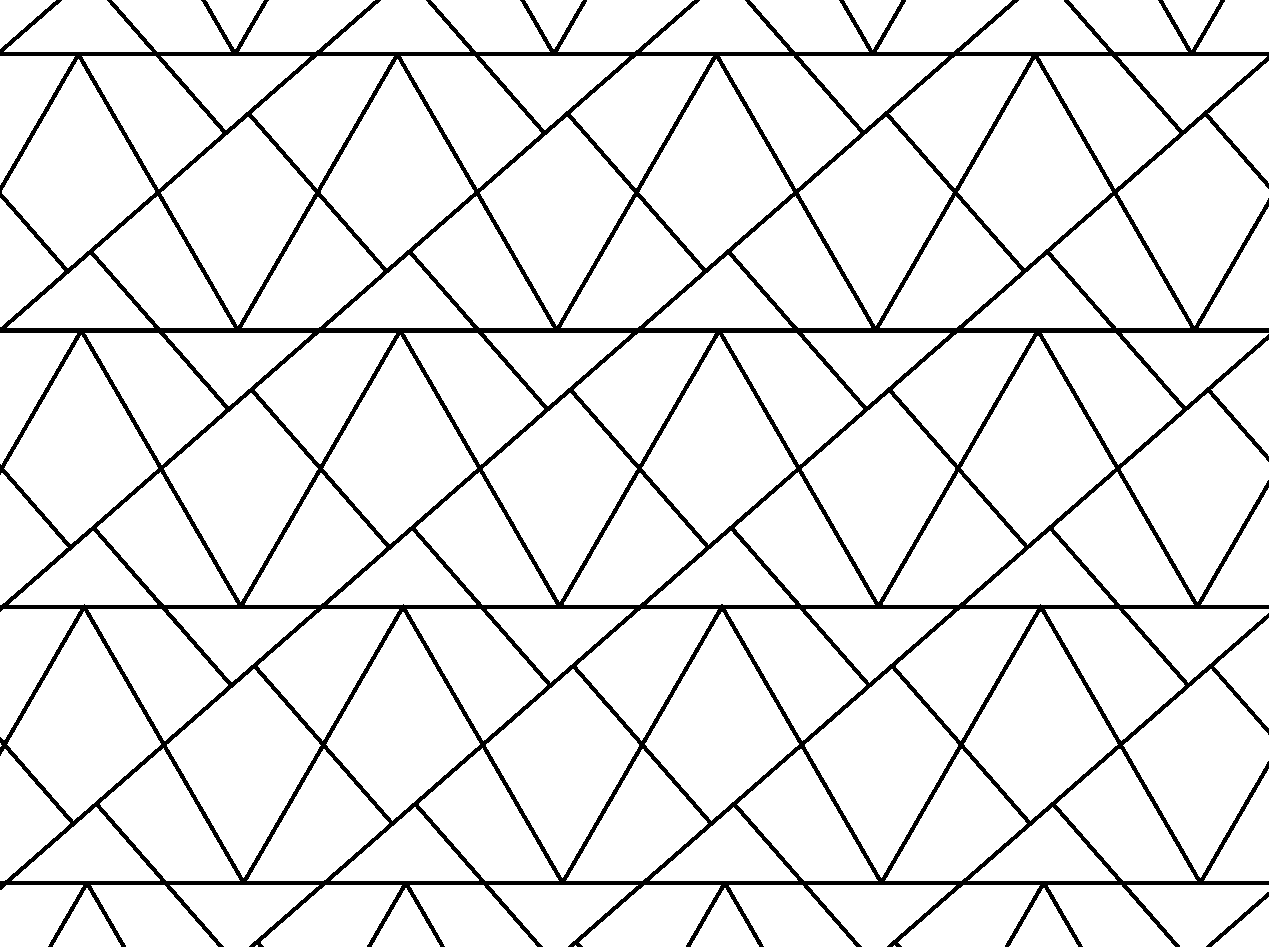
圖7. 錯位的鑲嵌帶形成平面鑲嵌
裁縫師問題的切痕有許多不同的等價作法,以上僅列出其中一種。這個作法也可以用尺規作圖完成。
這種將圖形切開後再組裝為新圖形的方法,在數學上稱為「幾何解剖」(Geometric Dissection),是計算幾何學(Computational Geometry)下的一個分支。筆者相當中意這個命名法,所謂「解剖」泛指研究、拆解並分析生物器官的學問。這種問題不也像是讓三角形、正方形像是有了生命一樣,可以去分析它們的構造嗎?
另外,如果我們將P、Q、R、S這四點中的其中三點固定,就可以像樞紐一樣旋轉,這種每塊拼圖都可以一塊一塊旋轉的構造,又稱為樞紐解剖(Hinged Dissection)。見下頁圖:
看啊!這不就變成了使用裁縫師問題的四塊拼圖所形成的新鑲嵌了嗎?由兩種鑲嵌帶疊合出的雙重鑲嵌,這也是裁縫師問題在幾何解剖學中之所以基本但特別的原因!
有趣的是,如果將四片拼圖染色,可以做出更有震撼力的鑲嵌。現在將裁縫師問題的四片拼圖各取四個顏色,並依照下圖的方式用樞紐連接的方式組合成四套拼圖:
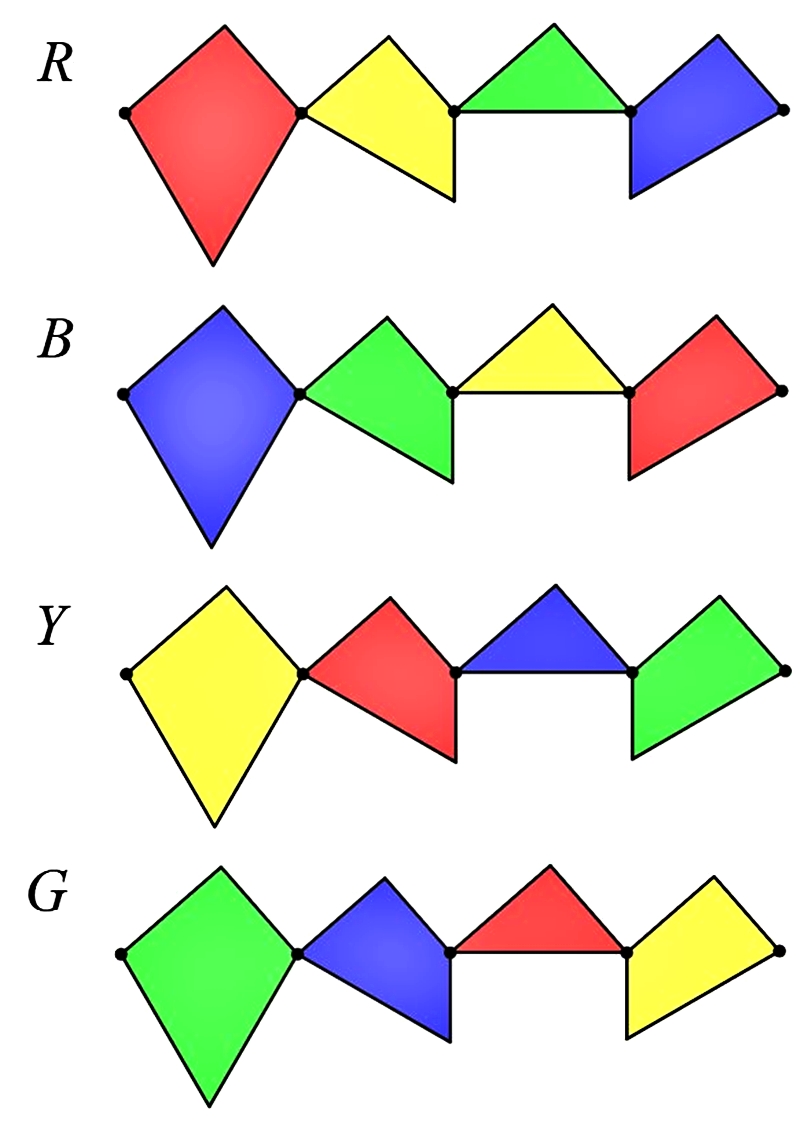
圖8. 四套拼圖(編號以最大塊的顏色命名)
接著,我們就有了兩種玩法,將四套拼圖全部組合成正三角形或是正方形的同一種,並且選取一個顏色,將四套拼圖同色的色塊全部靠在一起。會驚人地發現:當四片拼圖的「形」為正三角形時,將同色的色塊靠近會成為正方形;而當「形」為正方形時,將同色的色塊靠近會成為正三角形!
詳見下頁圖:
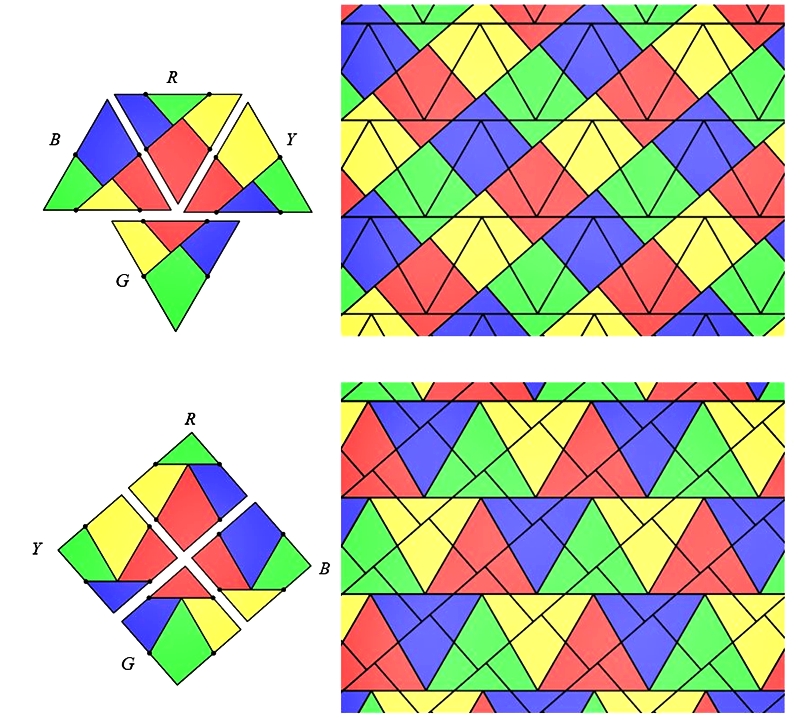
圖9. 裁縫師問題的「形」與「色」
至於每種鑲嵌都有這麼精彩的結果嗎?答案是否定的,這又更加一層地深化了裁縫師問題的特別之處。筆者認為,正如三角形在幾何學中擁有最多的特性,最基本的圖形反而有最奧妙的變化,裁縫師問題正是這句話的體現。
接下來,我們要將這兩種鑲嵌加入線性變換(linear transformation)的調味料,並且以另一個角度理解裁縫師問題。
預備知識三:康威生成子
我們重新觀察裁縫師問題的解。下圖中,不論是正三角形或是正方形的狀態,用來當作樞紐的四個點恰好可以構成一個非常近似於長方形的平行四邊形(銳角內角約為 )。我們將圖7鑲嵌中的每個平行四邊形都連接起來,會發現這些平行四邊形恰好生成一組鑲嵌!(註2)
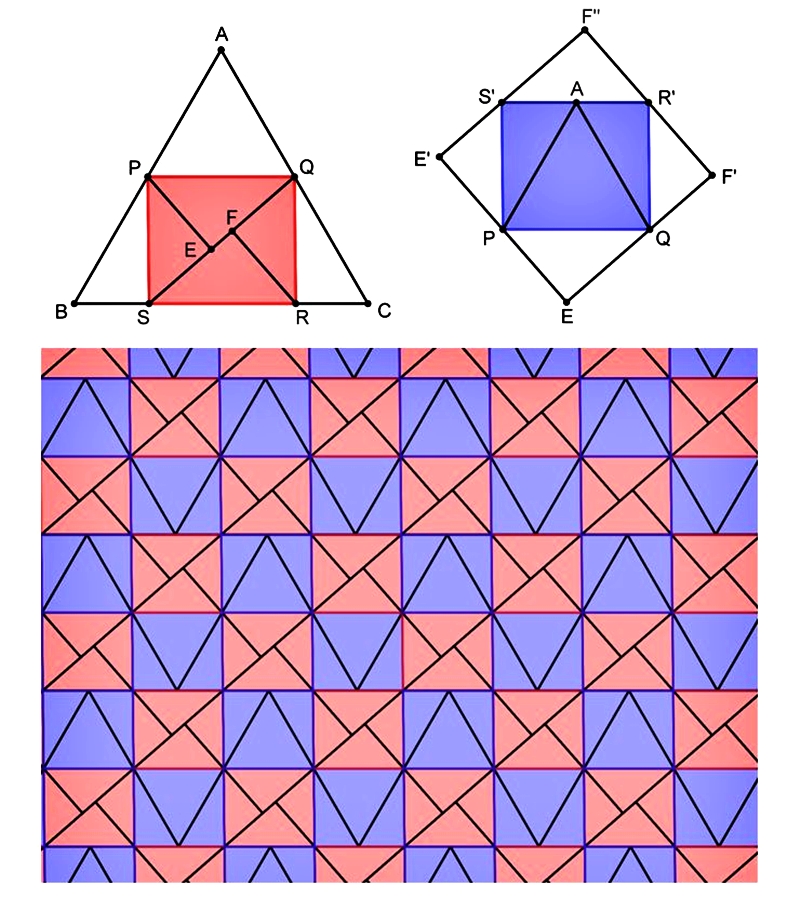
圖10. 切出平行四邊形
觀察上圖,這兩種平行四邊形如同西洋棋盤的上色法般交錯覆蓋在裁縫師鑲嵌上,這跟我們要討論的議題有關嗎?
這邊舉個實作的例子:
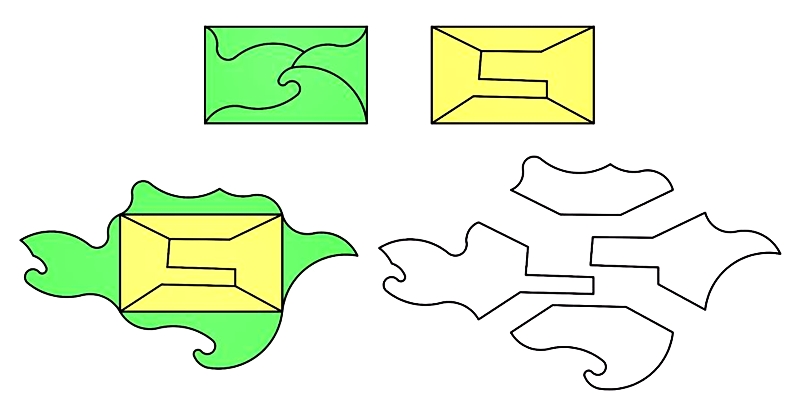
圖11. 任意的四片拼圖製作法
將綠色長方形的四個頂點互相用線連接,規定每個頂點恰好被碰到一次,並且這些線不能夠碰到長方形的邊,也不可以圍出不包含長方形邊界的區域。接著將綠色長方形沿線剪開成四片,往上、下、左、右翻面後貼合在黃色的長方形邊緣。最後將黃色長方形的四個頂點連接並剪開,抹去貼合邊,四片拼圖就完成了。
這四片拼圖剛好可以對應一組類似於裁縫師問題的幾何解剖問題。如何將下圖的「恐龍」切成四片拼成「飛碟」?
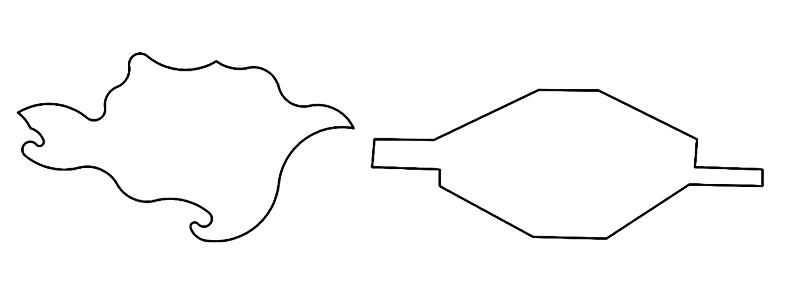
圖12. 「恐龍」和「飛碟」的幾何解剖問題
您看,如果我們不知道這兩張圖其實是由同一個長方形所產生的,就會變成一個極度困難的幾何解剖問題。
另外,如果我們像圖11一樣維持切痕,並且將圖形複製無數次,就可以形成下圖的鑲嵌。

圖13. 「恐龍」和「飛碟」的鑲嵌
我們將以上的知識進行整理:用兩個長方形製作成的拼圖,既是樞紐解剖,又是鑲嵌圖形,這不是跟我們的裁縫師問題有一樣的性質嗎?這樣子的長方形稱為康威生成子(Conway generator,コンウェイ.ジェネレイター)。重點是,康威生成子不一定是要長方形,平行四邊形也有一樣的性質。
請您與圖10的鑲嵌比較看看,可以發現,原來裁縫師問題的原理就是以兩個平行四邊形做為康威生成子,以特定的方式剪開形成的!
文章到此,我們以各種不同的面相解析了裁縫師問題的原理,剩下一個問題:這跟貓咪到底有什麼關係?請您回到前面,觀察一下圖1和圖2的切痕,不覺得兩者是一致的嗎?是的!筆者的貓咪圖案正是以裁縫師問題為本體,改造切痕完成的。
那要如何改造切痕才可以造成貓咪的效果呢?或是說,如何設計一個有意義的圖案?這就要進行到我們最後的預備知識,鑲嵌藝術大師──艾雪的技巧。
預備知識四:艾雪的鑲嵌藝術化
荷蘭的藝術家艾雪,將幾何鑲嵌的結構,結合「平移」、「旋轉」、「鏡射」以及「縮放」等等的技巧,將之融入藝術中構造出一幅又一幅的精采構圖。

圖14. 艾雪的鑲嵌作品示例
筆者以自己理解的方式,將其中一種技巧模組化,介紹如下:
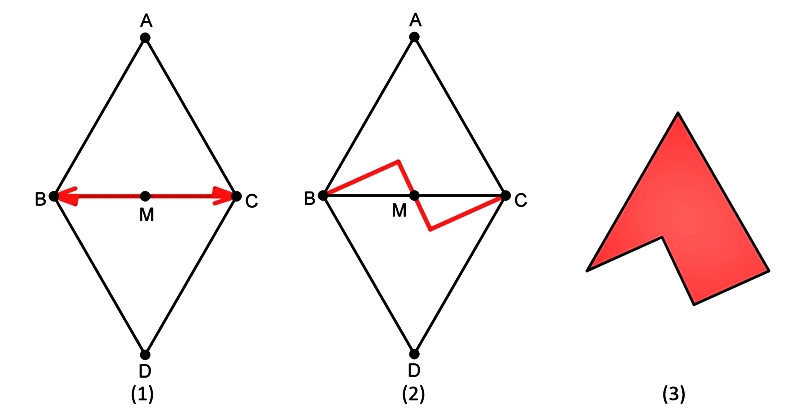
圖15. 藝術化碎片的製作過程
在兩片正三角形ABC、DBC的共用邊BC上,取其中點M。畫出向量MB、MC ,注意這裡的箭頭兩側的形狀是不一致的,這是用來強調MB、MC 互為點對稱圖形。接著,如圖15(2),沿著 隨意劃出一個切痕,接著將該切痕以MB為中心旋轉 ,沿著MC 畫出該切痕的點對稱圖案。此時可以發現,這兩個三角形同時被切成上下兩片形如圖15(3)的形狀。這代表的意思是,我只要將圖15(3)的形狀放置在正三角形格網上,就可以形成一套密鋪圖形。

圖16. 簡易的藝術化鑲嵌
大部分在網路上或是書籍上查尋到的技巧,都是以一個多邊形為基礎,將其中的一邊平移、旋轉、翻轉改造而來。但筆者認為這樣做有幾個缺點:第一,無法確定最後會拼成什麼樣的鑲嵌,或是到底能不能夠形成鑲嵌,特別是如果同時使用到「平移」、「翻轉」等兩種以上的技巧就會更容易出錯。第二,即便圖形是可以完成鑲嵌的,將圖形大量複製後有時會無法確認哪一邊要對齊哪一邊,就會造成製作的困難或是讓規則亂掉。第三,製造鑲嵌的這個動作,對於沒有經驗者非常不友善,特別是旋轉這個動作很容易造成挫折。
筆者為了避免以上情形,決定一次處理兩個以上的圖形,在鑲嵌的狀況下直接改造,一旦動了其中一個三角形,另一個的變化就會同時產生,讓製作的過程有了「藍圖」,這樣一來就可以直接看出最後會形成怎麼樣的圖案。綜上所述,本技巧的精神是:將正三角形的正鑲嵌網格沿著邊緣去改造,將一個正三角形的一部份剪下,沿中點旋轉拼貼後形成新的圖形。
最後,「正三角形」、「鑲嵌」、「旋轉」、「拼貼」,這些關鍵字不就是裁縫師問題的核心概念嗎?我們的預備知識已經齊全,「貓」即將要誕生了!
貓
在正三角形格網上,選定一個正三角形,並且標註出三個邊上康威生成子的四個頂點,也就是裁縫師問題的樞紐位置。以這四個點為中心,向三個頂點畫出四個顏色的箭頭以及對應的點對稱箭頭,這裡的四色箭頭就代表著要改造成貓咪的四個位置。
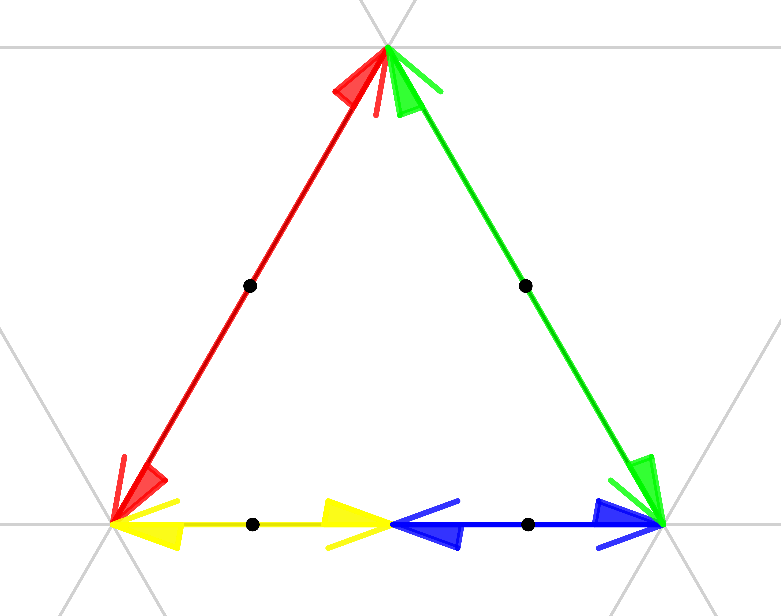
圖17. 製造貓咪的「藍圖」
接著,依序將紅色的部分改造成貓頭,綠色的部分改造成貓屁股,黃色的部分改造成貓腳,藍色的部分改造成貓肚,就完成了!
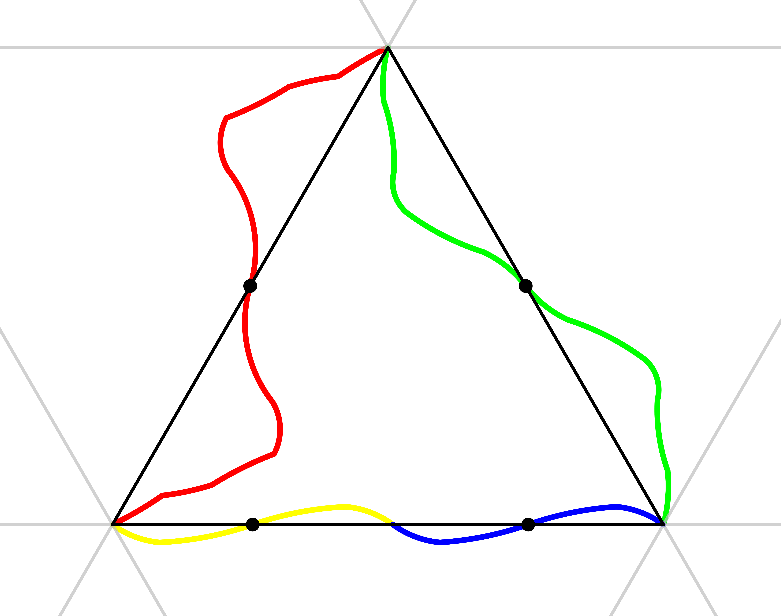
圖18. 貓咪完成圖
藝術化的步驟需要大量的累積錯誤來完成,筆者在研究各種改造方法時恰好發現了,貓的側臉旋轉 後和前腳很合拍,貓的後頸旋轉形成的背部很自然,腳部和肚子則是順勢調整完成,可惜很遺憾地沒有辦法做出個圓滾滾的貓屁股,這跟曲線的凹凸性有關,最後不得不妥協讓牠變成「屁股尖尖坐不住」。
好的,我們已經知道了這隻貓其實就是由裁縫師問題改造來的,我們就來看看牠有多千變萬化吧!
貓即是箱,箱即是貓
我們將圖18的貓咪沿著外框剪下,並且依照裁縫師問題的解答剪成四塊拼圖。這裡複習一下做法:將右上和左下的兩點連出線段,接著將左上和右下的兩點各自對該線段作垂線,即告完成。
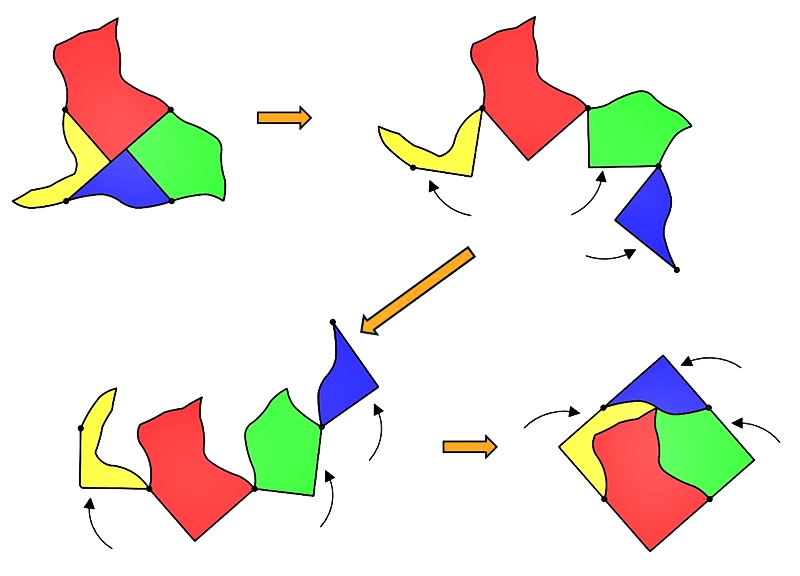
圖19. 貓咪樞紐解剖
回應文章一開始的問題,可以將一隻貓咪切開並重組為正方形嗎?可以!還可以做成樞紐解剖呢!另外,這裡選用的旋轉樞紐跟文章一開始的裁縫師問題是不同的,除了固定貓頭比較清楚之外,也是想讓您知道,其實以康威生成子四個頂點中的任三點當作樞紐都可以完成這個樞紐解剖。
回應文章一開始的問題,可以將一隻貓咪切開並重組為正方形嗎?可以!還可以做成樞紐解剖呢!另外,這裡選用的旋轉樞紐跟文章一開始的裁縫師問題是不同的,除了固定貓頭比較清楚之外,也是想讓您知道,其實以康威生成子四個頂點中的任三點當作樞紐都可以完成這個樞紐解剖。
貓中有箱,箱中有貓
用四個顏色將貓咪的拼圖染成紅、黃、藍、綠四色並且拼接,如果拼圖組成貓的形狀,則這時候四隻貓圍出的中心就會出現一個四色的正方形;如果拼圖組成正方形的形狀,則四個正方形的中心就會出現一隻四色的貓。
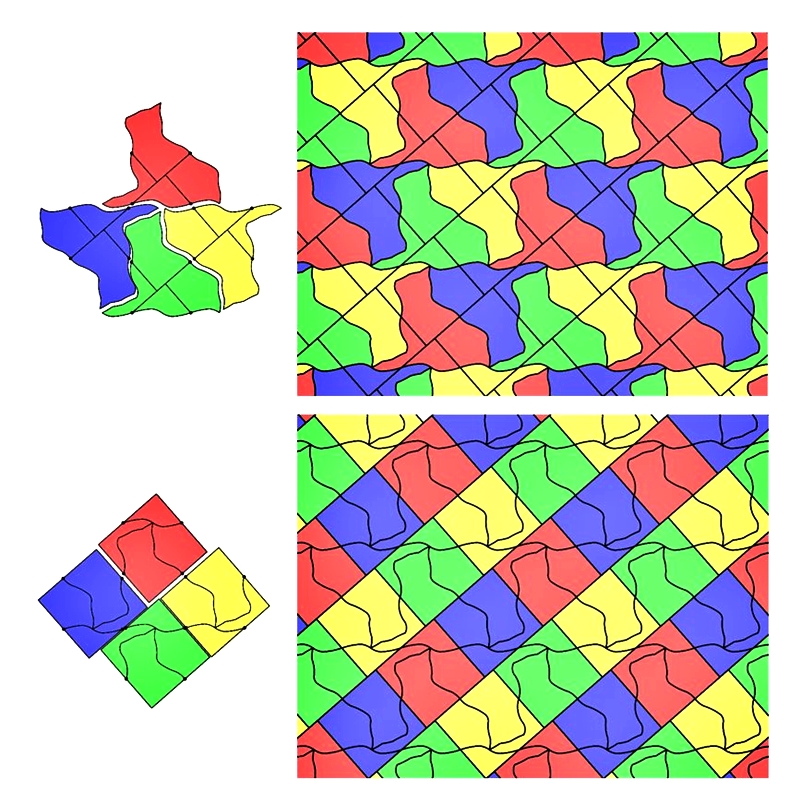
圖20. 貓咪與正方形的「形」與「色」
這裡和圖9的染色法不太一樣,除了是想告訴您不論將拼圖塗成四色或單色都可以玩四色鑲嵌,另外是筆者個人覺得貓咪染成單色比較有整體感。
結語
筆者是在幾年前因為一些契機,開始愛上解剖與鑲嵌的。
筆者為了設計遊戲,自己給自己出了一道題目:如何將一個正六邊形切成幾塊,並且重新組合成一個正六角星?當年完全無法破解這個題目,因為兩者的邊常比是無理數,怎麼想都不可能。後來接觸到裁縫師問題,一見驚為天人,這世界上竟然存在這麼美妙的作法!而且這也是筆者第一次接觸到一個數學問題,連怎麼開始第一步都不知道。
在研究的過程中,接觸到了美國數學家Frederickson的一系列解剖幾何書籍,讓自己感覺像是找到了失樂園,這是個幾乎沒有人涉足的領域。
後來,在2018年的數學年會上,有幸與日本的秋山仁老師有了一面之緣,聊天之餘得知了他也是解剖幾何的大師。買了他的書後,更深入地理解到解剖與鑲嵌的重要關聯性。書中就有將康威生成子組合成魚和蜘蛛的作法,筆者就很好奇,到底要怎麼創作出一個有意義的解剖圖案。後來經過百般鑽研,才終於生出了這隻貓咪,也才有了這篇文章。
筆者非常希望這個領域的數學可以在台灣拓展開來,讓每個人都可以嘗試做出屬於自己的解剖與鑲嵌作品。
致謝
本文的完成要特別感謝Facebook「藝數摺學寫作社團」的夥伴們給予的指教與建議,特別是楠梓國中顏敏姿老師、鳳山高中連崇馨老師以及林口國中李政憲老師(依時間序),感謝提供許多不同的觀點以及協助校正文章。
張惟淳
臺南市後甲國中教師
【備註】
1. 這裡取的∛4即為正方形的邊長,簡單計算如下:
正三角形的面積為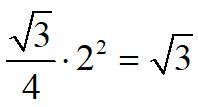 ,與正方形的面積相同,故邊長為∛4。
,與正方形的面積相同,故邊長為∛4。
2. 這裡的89.4°相當接近直角,十分有趣,補上簡單的計算:
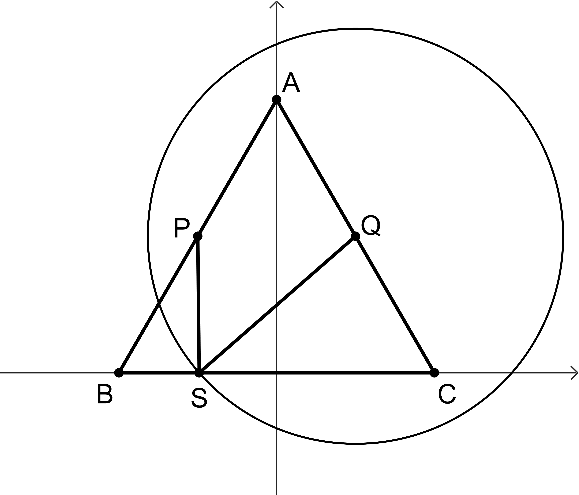
將邊長2正三角形ABC置於坐標平面上,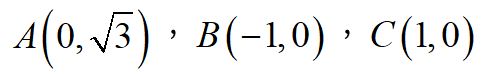 ,兩邊中點
,兩邊中點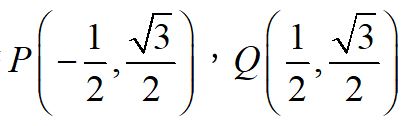 。以Q為圓心,∜3作圓:
。以Q為圓心,∜3作圓: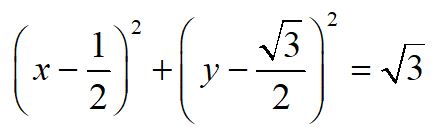 交 𝑋軸於
交 𝑋軸於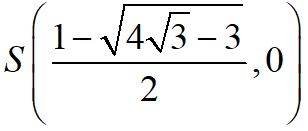 ,得
,得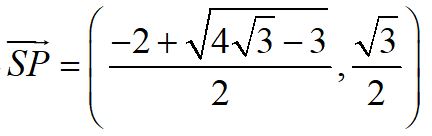 ,即可推出
,即可推出 與
與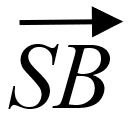 的夾角為
的夾角為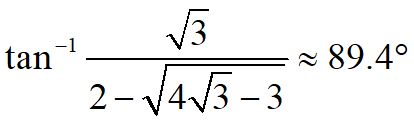
參考資料
[1] 藤田伸(2017)。圖解圖樣設計。易博士。
[2] Greg N. Frederickson(2017), Dissections: Plane & Fancy. CAMBRIDGE.
[3] Greg N. Frederickson(2010), Hinged Dissections: Swinging & Twisting. CAMBRIDGE.
[4] 秋山仁(2020)。離散幾何学フロンティア: タイル・メーカー定理と分解回転合同(離散幾何學開拓:鑲嵌生成定理與分解回轉全等)。近代科学社。
[5] Robert Fathauer(2021), Tessellations. CRC Press.
[6] Gavin Theobald(2021), Geometric Dissections. 檢自http://www.gavin-theobald.uk/ (Feb 19, 2021)
[7] 艾雪的鑲嵌圖片取自網路:
飛馬:https://tinyurl.com/2p9sym8m
蜥蜴:https://tinyurl.com/2af3ybp3
本文引用格式:張惟淳(2023)。貓是液體!鑲嵌與解剖的幾何魔數。科學研習,62(1),38-55。