
文/李政憲、李慧玲
筆者成立「藝數摺學」社團以來,發展過不少的摺紙數學相關活動,廣受教師、學生與一般民眾喜愛。「哥倫布方塊」正是一個可以從小玩到大,從最簡單的摺製與堆疊(如圖1),到最困難的體積與兩面角計算、不同凹角數的討論(如圖2),都是一個可以很容易上手,並且與數學作連結的好活動。之所以稱為「哥倫布方塊」的原因,是一個蠻有趣的軼事。本文將從其名稱開始介紹起,接著討論其摺製方式與哥倫布方塊球的組裝與摺製方式,同時帶各位讀者思考所需要的數學知識,以及最後延伸作品的展示,希望可以讓大家對於這個作品的相關知識有更深入的了解。

圖1.

圖2.
哥倫布方塊由來
話說於1492年發現美洲新大陸的哥倫布(Christopher Columbus,1451一1506)回到西班牙後,辦理了一場慶功餐會。在慶功宴上有人就很不以為然的說道:「我看這件事不值得這樣慶祝。哥倫布不過是坐著船往西走,再往西走,碰上了一塊大陸而已。任何一個人只要坐船一直向西行,都會有這個發現。」這時會場的氣氛尷尬極了,大家頓時鴉雀無聲,面面相覷,不知道如何回應。
只見這時哥倫布不慌不忙的站了起來,拿起宴會上一顆煮熟的雞蛋,慢慢說道:「請各位試試看,誰能使熟雞蛋的小頭朝下,在桌上站住?」很明顯無論大家如何嘗試,總是會滾來滾去,引起哄堂大笑,無法將其尖頭朝下,立於桌面上。
眼見大家無法挑戰成功,接著哥倫布便拿起這顆雞蛋,把尖頭往桌上輕輕一敲,那稍微碎了一點殼的蛋就穩穩地立在桌上了。這時剛剛講話的人不禁大叫:「這不能算,他把蛋殼摔破,當然可以站住。」只見哥倫布正色說道:「是的!你和我的差別就在這裡,你不敢敲,而我敢敲。世界上的一切發現和發明,在一些人看來都是簡單不過的;然而他們總是在別人指出應該怎樣做以後才會說出來。」最後贏得宴會上每位賓客的喝彩。
很有趣且勵志的一個故事是不是?在還沒開始活動之前,就可以先跟學生勉勵一下,一個任務是否成功的重點在做與不做,接下來的每個活動,如果你正猶豫要不要做,或是不知道如何下手,不妨回想這個故事,說不定就可以鼓勵自己持續完成挑戰,往下一個任務邁進【註1】。
我們要摺製的作品為什麼跟這個故事有關呢?請各位讀者不妨看一下圖3左圖,很明顯的是一個正方體,若將此正方體內凹一個角為中圖,你會發現內凹的部份將形成一個三角錐,其底部將形成一個正三角形。若我們將此正三角形底部朝下放於桌上,就可以形成右圖正方體斜放於桌面上的效果,與故事中提到的雞蛋尖頭朝下有類似的效果。

圖3.
接著下個部份,我們將逐步說明這個作品的摺製方式,並接著討論其相關的數學知識內容。
哥倫布方塊摺製【註2】
基本元件1.0版摺法
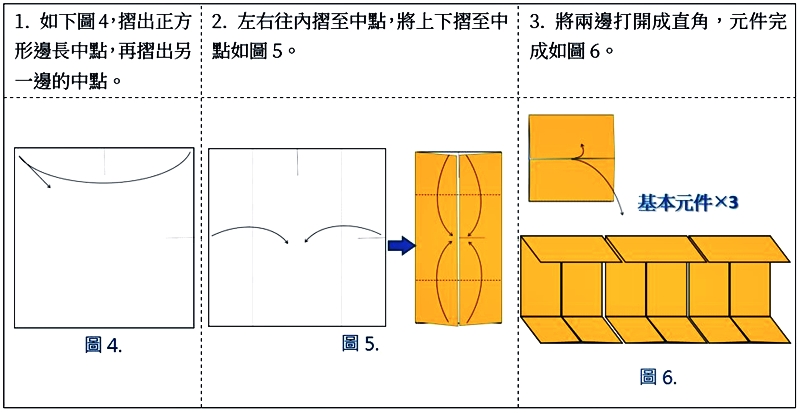
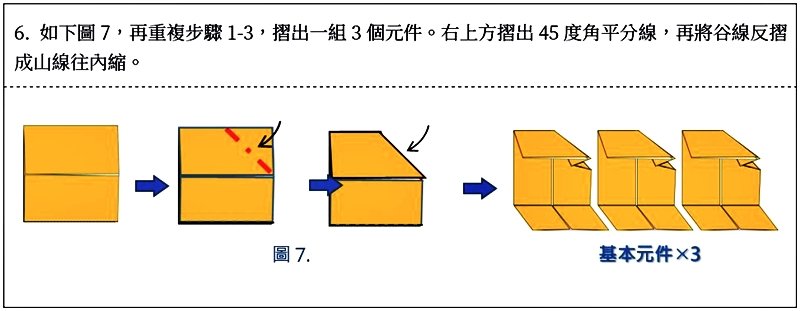

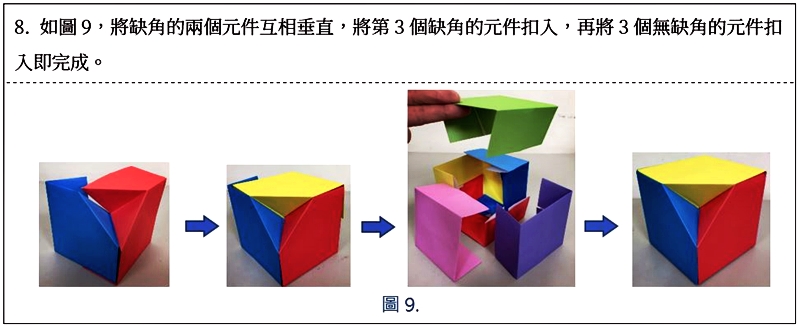
利用1.0版摺法所組合出來的哥倫布方塊,因為有3個面沒有凹摺互相卡住,較容易有鬆脫的情形出現,為了修正這個缺點,經由「藝數摺學寫作共備群組」相關老師們討論,我們發展出以下2.0版的摺法。
基本元件2.0版摺法
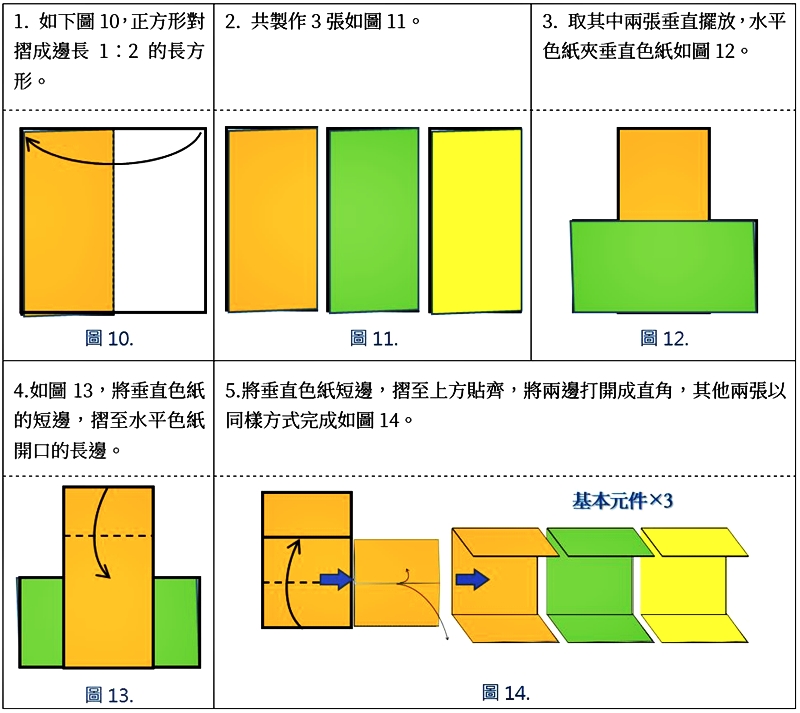
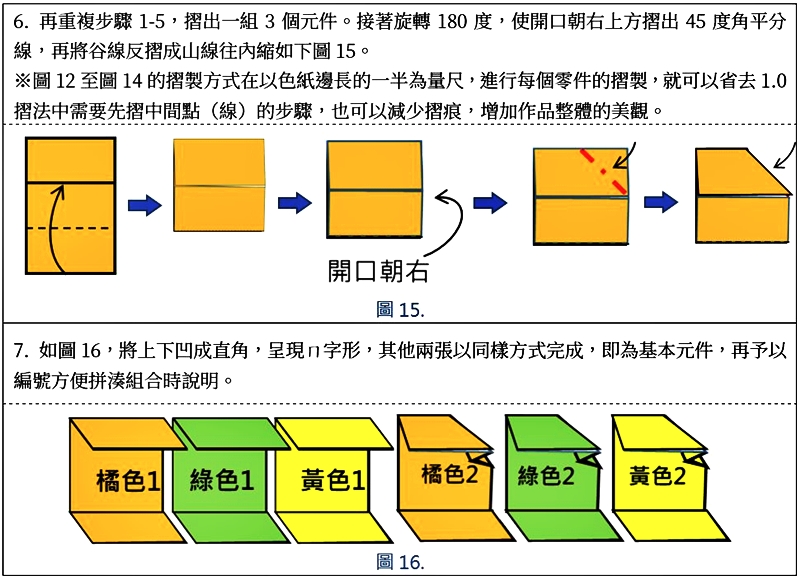


比較1.0版摺法與2.0版摺法有什麼不同?1.0版的摺法組合結構不穩定︰2.0版和1.0版最大的差別,是在於我們對摺之後,可以把開口從中間移到旁邊(如右圖24)。
所以每一個元件都有一邊有開口,此開口可以讓相鄰面元件的摺疊部分,插入放進兩夾縫中,每個元件只有一個開口,6個元件每個元件都有一個摺疊部份可以塞入夾縫中,這樣互相牽制之下讓結構不容易鬆脫,形狀更為穩定。所以如果要進行堆疊的活動,建議可使用2.0的摺製方式,在方塊倒下後比較不會散掉。如果教師要進行教學,建議先進行1.0的教法,再作2.0的教學,除了讓學生比較其差異性,學生也比較容易產生學習遷移與上手。
2.0版因為有一面是開口,在組合時就會擔心開口的位置不同,元件是不是會無法維持每個元件都互卡?結果發現,前三個元件在互卡組合時,開口方向可以自行任意決定,剩下三個元件組合的開口位置會唯一,可以依序組合好。
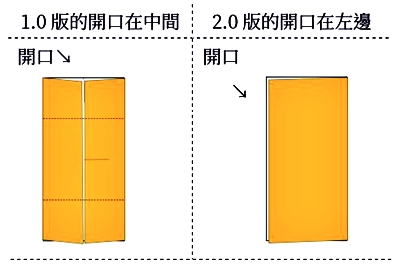
圖24
哥倫布方塊凹角討論與哥倫布方塊球製作
接下來我們要討論哥倫布方塊的凹角方式,接著完成20個哥倫布方塊所組成的哥倫布方塊球(如下圖25)。我們發現每一個方塊與其他方塊恰有三個頂點相連接,其連接方式正與凹角相對位置是相關的。

圖25.

圖26.
我們先探討以下幾種立方體凹角的數量與所在頂點位置:
表1.
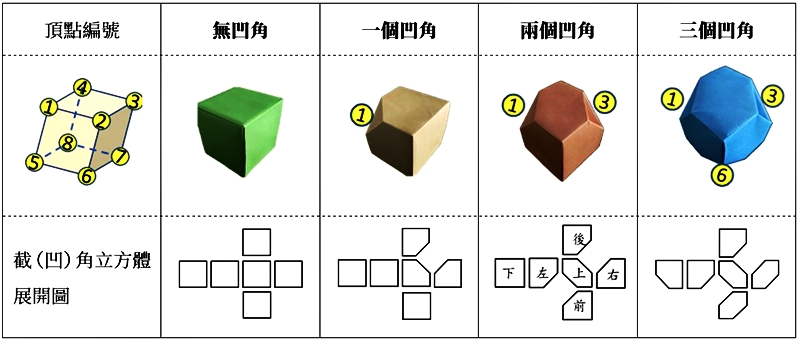
立方體凹角的位置與數量如上表1。
假設我們製作第1個凹角的位置在頂點1,如果在與1相鄰的三個頂點2、4、5做凹角,我們發現若要將立方體黏合成環(如上圖26,因要黏合成環才能依此概念結合成球,詳見註3),兩個立方體將會互相碰撞(如右圖27),無法組合。如果在對角頂點7,兩個立方體則會形成直線關係,亦無法形成環狀,而且這兩種接法與上圖所示哥倫布方塊球的接合點也不符。於是我們剩下頂點3、6、8的位置可供選擇,若選擇頂點3為第二個凹角,剩下來的頂點6和頂點8任一個納入後,都會符合選擇三個截角處的凹洞不會相互碰撞的特性,因此這兩個頂點擇一即可。結論是1、3、6、8四個頂點若我們任選三個作為立方體的凹角,共有4種(1、3、6)、(1、3、8)、(1、6、8)與(3、6、8)的不同選法。

圖27.
因此若我們要製作一顆哥倫布方塊球,根據上述討論的凹角位置,不妨從一個立方體的一個頂點出發,在表面畫正方形的對角線三次,三條對角線將回到原頂點,且這三條對角線所經過的3個頂點恰為三個凹角的位置,三個頂點將形成一個正三角形。
我們不妨觀察一下底下圖28的正十二面體結構,五個單一凹角立方體所連接成的環(如前頁圖26),五個立方體可以視為正五邊形的五個頂點(如右圖28),因為製作一個哥倫布方塊球共需20個立方體,與正十二面體的頂點數相同;且每個立方體均有三個頂點與其他立方體互相連接;每兩個相鄰方塊的共用頂點會產生一個凹角(一凸一凹),我們不妨將這一凸一凹連接處視為以正十二面體的邊作連結,故頂點連接處共30個,亦即共需30個凹角。
由此得知哥倫布方塊球的結構恰與正十二面體是同構的,因此若我們將各立方體的凹角相連接,可視為每個立方體放入正十二面體的20個頂點,且正十二面體的邊,將對應每個方塊三個連接點與相鄰的方塊相連接,且一個凹角恰會搭配一個未凹陷的頂點進行組合。
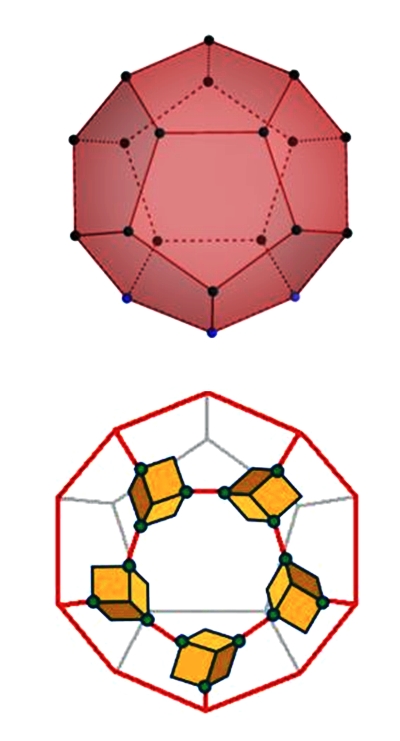
圖28.
我們接下來將透過正十二面體的透視投影結合方塊的凹角數,繼續討論其不同的連接方式。
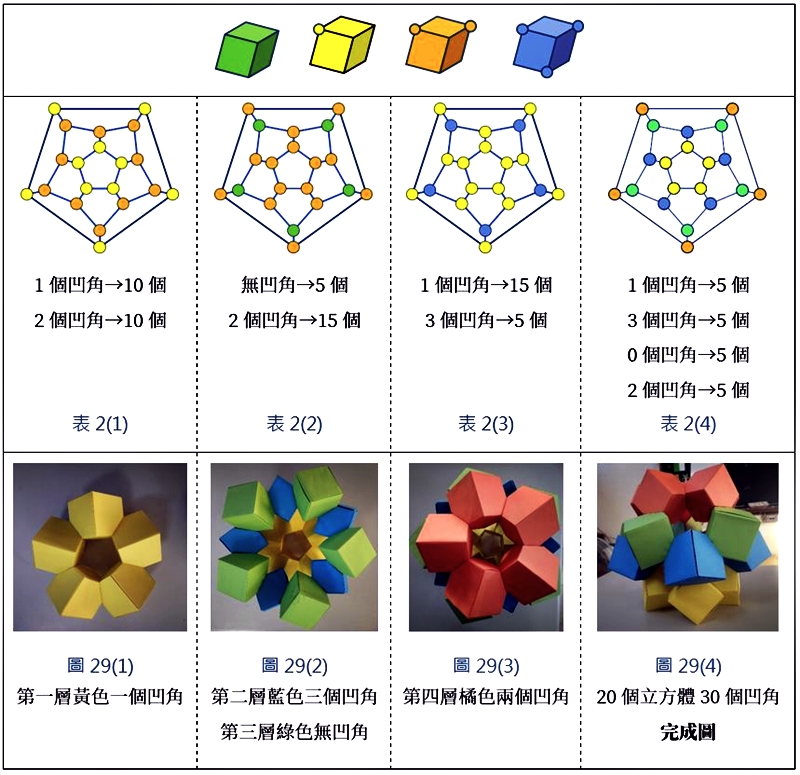
我們發現組合的方式很多,其中以五個一層的方式較易觀察,因為總共有四層,以下表2的簡圖示意。我們列舉了正十二面體頂點搭配方塊凹角數的其中四種組合,圓點代表立方體的位置,綠色圓點代表方塊無凹角、黃色圓點代表一個凹角、橘色圓點代表兩個凹角,藍色圓點代表三個凹角。有興趣讀者不妨可延伸探討,各種組合搭配不同凹角數,與立方體數量的增減關係。
我們發現凹角立方體至少需要兩種,如下表2(1)即為10個一個凹角的立方體,另外10個是兩個凹角的立方體;而表2(4)每層都是同一種凹角數量的立方體,四種凹角的立方體數量均為5個。以下我們將接著說明兩個凹角的立方體的摺製方式,請讀者們不妨可依圖29(1)~29(4)摺製1、3、0、2個凹角的方塊各五顆,依表2(4)中的組合方式黏合成一組哥倫布方塊球(底下將接著示範兩個凹角的方塊摺製方式),並試想其他組合應該如何摺製與黏合?
兩凹角哥倫布方塊摺製說明
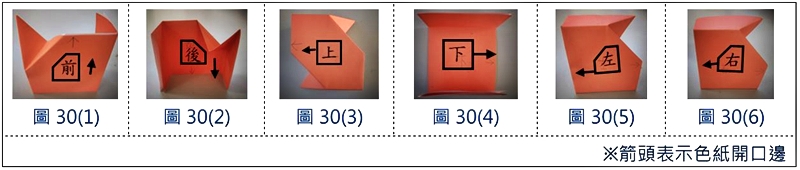
最後我們再示範如何以色紙進行兩凹角的哥倫布方塊摺製。為了加強各位讀者完成方塊的強度,我們這裏採取本篇文章所提2.0方式摺製同一平面上的兩個凹角,如果忽略開口夾住元件,即為1.0的方式摺製。請各位讀者依圖30(1)-30(6),先摺製六個零件,再依圖31-圖36組合為最後成品即可。有興趣的讀者們不妨可以仿照兩凹角的摺製方式,接著挑戰三個凹角的方塊摺法(可參考表1不同凹角數所摺的相對位置),即可搭配不同連接方式進行組裝黏合。

其他延伸討論
除了本文所進行哥倫布方塊凹角與哥倫布方塊球的討論與實作,在中學教學時,哥倫布方塊的實作還可以進一步討論其堆疊的高度、單顆的體積與圍繞成環的兩面角計算,從等差數列、相似形、錐體與柱體體積計算與兩面角的討論,著實能以這個課程將中學的幾何課程作個綜合性的統整。在此建議若孩子僅國小程度,不妨先比較1.0與2.0的摺製方式差異,並進行堆疊高度的挑戰;若為中學以上,則視其先備知識,陸續將其他可供討論的數學知識放入課程或教學之中。【註2】
如果還有興趣延伸摺紙課程的朋友,不妨可以再接著挑戰以下的幾個作品:

圖37.

圖38.

圖39.
-
以三條紙編方式完成一個凹角、兩個凹角與三個凹角不同凹角數的哥倫布方塊【註4】;
-
哥倫布方塊鑲嵌球(如圖37,引自藝數摺學社團,游曉琦老師提供,建議完成正方體邊長減半的哥倫布方塊環12個,再直接黏合於已完成的哥倫布方塊球上即可完成)
-
哥倫布方塊三角錐製作與堆垛問題討論(如圖38,建議先以色紙拼組或紙編完成六個等腰直角三角形面的六面體如圖39,一般在摺紙裏稱為fox cube,才能理解其結構並以黏貼方式完成方塊金字塔作品)。
-
惟以上部份作品的概念提來又將是不少篇幅,或許待日後有機會再跟各位讀者細談要如何完成以及其中的數學性了。另本文承蒙師大附中彭良禎老師與楠梓國中顏敏姿老師斧正勘誤,特此致謝。
備註
【註1】原始資料引自維基百科。然而哥倫布發現新大陸的同時,也產生了不少殖民地的衝突,甚至造成不少地方的腥風血雨。若學生的年紀較長,也不妨從負面的角度跟他們談一下新大陸的發現,其優缺點各為何,這就是另外一種課堂的操作方式。
【註2】摺法參考自科教月刊第432期「哥倫布方塊與費氏花」,游曉琦、吳惠美。另相關摺製簡報繪製由楠梓國中顏敏姿老師製作提供,特此致謝。
【註3】關於哥倫布方塊環的製作,實際計算的兩面角為cos-1(-1/3)≈109°,與認知中正五邊形的每個內角108度略有差異,不過因為摺紙時的彈性,可以用將就的方式予以黏合。有興趣探討的讀者們不妨自行研究,或是參考【註2】理解其結果。
【註4】有興趣研究的讀者們,可直接至「藝數摺學」臉書社團參考相關資料先行完成一個凹角的紙編哥倫布方塊,再思考如何完成兩個凹角以上的紙編方塊。
李政憲
新北市林口國中教師
李慧玲
桃園市中興國中教師
本文引用格式:李政憲、李慧玲(2023)。藝數摺學‧一個可以從小玩到大的活動:哥倫布方塊。科學研習,62(1),26-37。