文∕李源順
數學就是無限的科學。“Mathematics is the science of the infinite.”
Hermann Weyl, 1930
在數學上，無限（infinite）或者無窮是一個重要的概念，但許多人對它的認識不是很清楚， 或者不認同，因此在數學的學習上變得比較困難。
生活上的無限
在生活上，我們可能聽到無期徒刑，它雖然是終身監禁的意思， 但是它不是一直都要執行永無停止的制度，最多只到犯人老死為止， 甚至被判處無期徒刑的犯人，在台灣，2005年以後在監獄中執行25年以上且達到一定的條件， 就可以啟動假釋制度。因此從數學的角度看，無期徒刑不是「無期—沒有期限」。
有人認為一個人的一生，頭髮的數量是無限的，因為它掉了還會再生長出來。 可是從數學的角度，頭髮的數量還是有限，只是很多或者不容易數而已。 因為當一個人離世以後，頭髮的數量便會終止生長，不會再增加。
因為無限是一種永遠無法停止的概念，在生活中幾乎看不到。即使是地球從生命的誔生到未來的毁滅，雖然要歷時非常非常久，但是還是一個有限的時間，因此人們在生活中很難感受到無限的概念。
數學上的無限
本文在此僅以0.9為例討論有極限（limit）的無限問題和數系的個數有無限多個為例討論無限大的問題。極限的概念是微積分的重要概念，不了解它，微積分便很難學得好。
一、0.9=1嗎？
高中生都會學到0.3=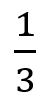
，且相信它是對的。因為它可以用1除以3，一直除下去，永遠無法停止，因此它是一個循環的無限小數問題。但是許多學生不相信0.9=1。作者曾經問過28位數理系一年級大學生，發現只有一半的學生認為0.9=1；46位大學幼教系和特教系一、二年級學生，只有五位（11%）認為0.9=1。其他都認為0.9<1，而且都說0.9只是趨近於1，還比1小一點點。認為0.9=1的學生都說以前老師用下面的方法教他們證明過：
設x=0.9999...①
10x=9.999...②
②-①得
9x=9
所以x=1
從數學知識的角度剖析0.9=1的概念，發現它是一個極限的概念。我們可以造一個數列{an=0.99…9（有n個9）}，此時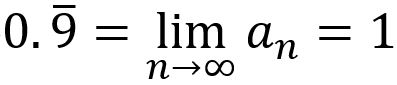
。當我們在解釋
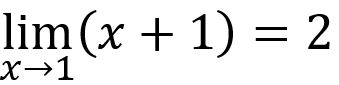的極限問題時，也時常令x=0.9，0.99，0.999，…，來讓學生感受x愈接近1時，x+1會愈來愈趨近於2。因此0.9是極限的概念卻沒有極限的形式，所以它是一個很難理解的問題。在這邊也要注意的是：n→∞，an→1表示它們只是趨近，但永遠不會等於1，但是當我們用lim來寫的時候，表示它的極限值真的會等於1，也就是
。
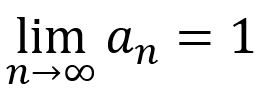極限的概念是微積分的精神所在，卻是一個很難了解的概念。在歷史上，Zeno（西元前490~430）的悖論也困惑世人一段很長的時間。其中有關二分法悖論（Boyer，1949；Kline，1972；引自李肖梅，1993）是這樣子的：
某一跑步者做如下的推論。在跑步者到達終點之前必須先經過路程的中點。然後必須再跑到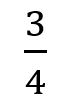
處，它剩下路程的一半。而跑步者在跑完最後的
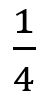之前，必須跑到這段路的中點。因為這些中點是沒有止境的，因此，跑步者根本不能到達終點。
當時的數學家面對這個隱含無限概念的悖論無法釋疑，直到十六世紀，極限的概念才建立完成。
極限的概念在中國也曾經被提及過。古代莊周在《莊子》一書中提出：「一尺之棰，日取其半，萬世不竭。」三國時代的劉徽利用「割圓術」計算圓面積時，也曾經說過：「割之彌細，所失彌少，割之又割，以至不可割，則與圓無所失矣。」這都是無限的概念。
為了讓學生了解0.9的無限概念，作者用各種方法問學生。
1. 運用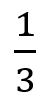×3
假如學生相信0.3=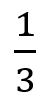，可以把它兩邊同時乘以3或者連加3次，此時0.3×3=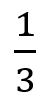×3，便會得到0.9=1的結果。
2. 運用1÷1的除法
假如我們稍微放寬計算除法時，餘數比除數小的規約，讓餘數可以等於除數，這時候會發現1=1÷1=0.9999…的結果。如下算式
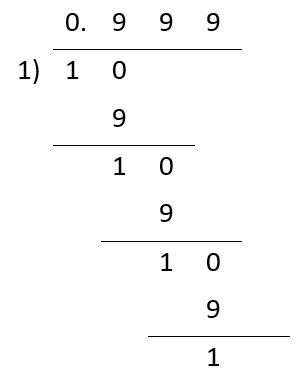
3. 兩相異數之間有無限多個數
作者還問學生，我們都知道任何二個相異實數之間有無窮多個數，因為我可以把這二個數相加再除以2，就找出它們的中點。假如0.9<1，那麼找一個介於0.9和1之間的數就好。當學生發現他們找不到兩者之間的數時，有學生反而懷疑數學上說的「任何二個相異實數之間有無窮多個數」是不是對的。因為在日常生活當中兩個人或者兩顆珠子併排，其中再也擺不進去一個人或一顆珠子的經驗；我們把一條吐司用切一半的方式一直切下去，到後來會出現不能再切下去的直觀經驗。
4. 兩相異數相減
作者再問學生，我們解答兩數的大小問題時，時常利用兩數相減來處理，因此請學生計算1-0.9，學生會察覺答案是0.000…（0永遠寫不完），所以0.9=1，但有部份學生的答案會是0.000…1（=0.01），即小數點後面有「無限多個0」再一個1。但是「無限多個0」再一個1，與學生的事實認知「無限多個，就不可能有最後一個」相衝突。
在作者說明之後，大部份的學生相信0.9=1，但是仍然有一位學生說，「它是一個哲學的問題，信者恆信，不信者恆不信」。作者同意他的說法。
有一位學生在0.9<1與兩相異數之間有無限多個數的衝突下，選擇懷疑兩相異數之間有無限多數，而相信0.9<1。同時說明0.01是緊鄰0右邊的數，它們中間沒有其它的數了。
有興趣的讀者或許可以思考0.01的數是否真的存在？如何定義它的四則運算？運算的結果是否仍然符合數的體系？例如0.01+0.01=0.02。說不定反而可以創造出新的數學理論。
二、數系的個數一樣無限多嗎？
相信大家都同意自然數（N）的個數有無限多個，因為它可以一直往左進位，永遠寫不完。相同的，整數（Z）、有無理（Q）、無理數（Q）、實數（R）的個數也都是無限多個。
在數學的發展史，有關無侷限的無限問題，希爾伯特的旅館悖論就是和自然數有無限多個有關的問題：
宇宙中有一個無限房間的旅館，每個房間都住滿了客人。現在又來了一位客人要住進旅館，這時候旅館的老闆請住在1號房的客人搬到2號房，住在2號房的客人搬到3號房，…，住在N號房的客人搬到N+1號房。再請新來的客人住到1號房。這時候每一個人都還是有房間住。
數學家為了了解無限個數的概念或性質，從A、B二個元素個數是有限集合的性質，發現假如二個有限集合的元素個數相等，若且唯若可以找到一個函數f: A→B，同時f為一對一且映成的函數（也就是二個集合內的元素，可以一個對一個而且每一個都被對應到）。因為f為一對一函數時，保證A集合的個數小於或等於B集合的個數；f為映成函數時保證B集合的每個元素都被對應到，所以A集合的個數大於或等於B集合的個數，如下圖一。兩者同時成立，便可以保證A集合和B集合的個數相等。因此概念推廣此一有限集合的性質，定義二個無限元素的集合，它們的個數相等若且唯若可以找到一個一對一且映成的函數。
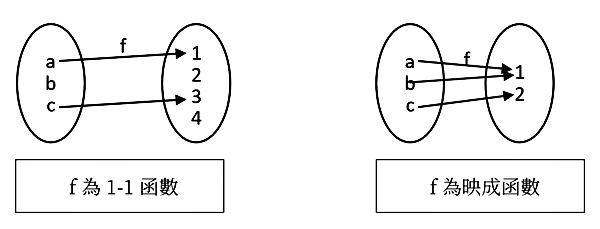
圖1. 一對一和映成函數示意圖
運用上述無限集合的定義，希爾伯特的旅館悖論問題得以解釋，可以定義f : {0} ⋃ N→N，其中f（n）=n+1, n∈{0} ⋃ N。也就是0, 1, 2, 3, 4…分別對應到1, 2, 3, 4, 5…。此時很容易可以證得f為一對一且映成的函數。在微積分的概念上，這個問題可以想成是∞+1=∞。
同樣的問題，直觀來看，整數的個數比自然數的個數多了一倍（負整數）又多1個（0）。但是我們可以
定義
f : Z→N，其中
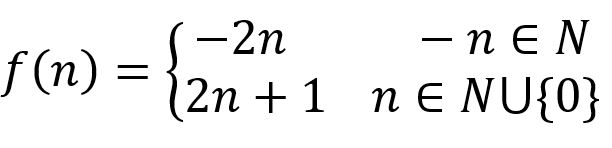
也就是…-2,-1, 0, 1, 2…分別對到4, 2, 1, 3, 5。此時也可以證得f為一對一且映成的函數。這個問題在微積分上可以想成2×∞+1=∞。
許多人會感覺有理數的個數比整數多很多，因為分子和分母都是整數。但我們可以找到一個函數
f :Z→Q，且
f (0)=0
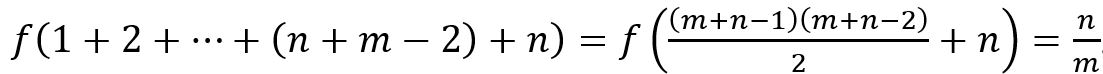
，其中 m, n∈N, mn≠0
負整數對應負分數的概念相同。
m+n=2且n=1時，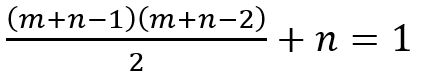
；
m+n=3且n=1, 2時，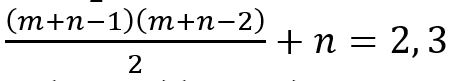
；
m+n=4且n=1, 2, 3時，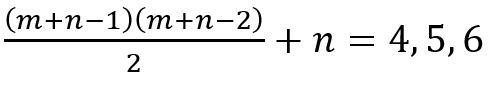
；
…；
表1. 正整數和正有理數的多對一方式
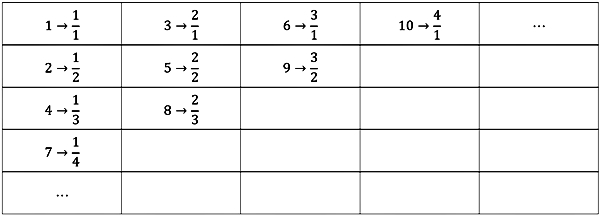
此時可能有多個整數都可以對到同一個有理數（等值分數），例如f (1)=f (5)=f (13)=1，但是每一個有理數都被整數對應到（映成函數），所以整數的個數比有理數的個數多或者相等。因此我們可以證得整數的個數和有理數一樣多。這個問題在微積分上可以想成∞×∞=∞。
很特別的是，雖然同樣有無限多個數，無理數的個數比整數的個數多太多了。它的證明需要使用到在數學上非常重要的矛盾證法。
假如存在一個一對一且映成的函數f :Z→Q，使得f (n)=Pn，其中Q={Pn |n∈Z}
現在令純小數P=0.a1 a2 a3 …，
其中a1 是第一位小數且異於P1 的第一位小數，
a2 是第二位小數且異於P2 的第二位小數，
a3 第三位小數且異於P3 的第三位小數，
…。
此時，P是異於P1 ,P2 ,P3 ,…的無理數。所以假設不成立，也就是找不到一個一對一且映成的函數，因此無理數的個數比整數的個數多。
事實上，可以更直觀的看，P1 , P2 , P3 , …的數列，Pi 的第i位小數只是0到9的其中一個數，因此異於Pi 的第i位小數還有9個，把所有的9個相乘，發現無理數的個數比有理數的個數多太多了。
在數學上，有一門測度論的學問，它告訴我們，把閉區間[0,1]的所有有理數形成一個點集合，再計算它的長度，結果長度為0。把[0,1]的所有無理數形成一個點集合，再計算它的長度，結果長度是1。可見無理數的個數比有理的個數多太多了。
邊長為1的正方形面積，從積分的角度是可以把長度為1的線段（面積為0）從0積到1，變成面積為1的面積，也就是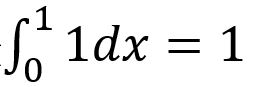
，它主要的關鍵點也就出現在無理數的個數上。也就是把長度為1的線段（面積為0）從0積到1的有理數時，它的面積仍然為0；把長度為1的線段（面積為0）從0積到1的無理數時，它的面積為1。
所以數學家把自然數、整數、有理數的無限稱為可數的無限，因為感覺上它是可以從1, 2, 3 , …一直數下去，而無理數、實數則為不可數的無限。
幾何學上的無限
我們都知道在座標平面上，是可以無限延伸的，因此坐標平面是無限的概念。當我們用動態軟體（例如GGB）畫雙曲線時，就會發現如下圖二，例如雙曲線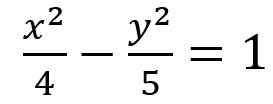
的參數式，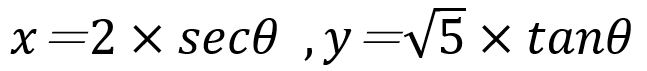
，當θ從0°走到90°時，雙曲線會從（2, 0）走到右上方的無限區域（圖二-1）；θ從90°走到180°時會從左下方的無限區域回到（-2, 0）（圖二-2；θ從180°走到270°時，會從（-2, 0）走到左上方的無限區域（圖二-3）；θ從270°走到360°時，再從右下方的無限區域走到（2, 0）（圖二-4）。如此一直循環下去。
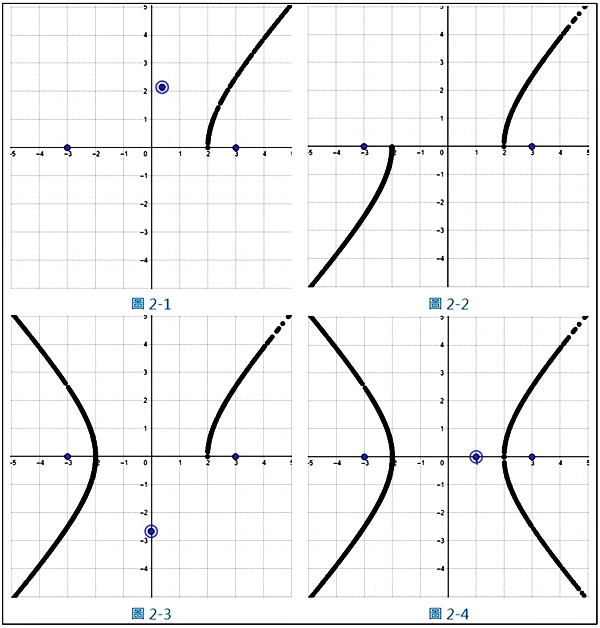
圖2. 雙曲線的動態軌跡圖
物理學和天文學上的無限問題
從物理學的角度，標準模型假設無法再加以分割的物質粒子有兩種，分別是夸克和輕子（林肯，2018），因此任何一個物質經過分割到最後就會是夸克和輕子，不能再分割下去，不能像數學一樣，任何兩個相異數之間有無窮多個相異數。但是當我們能製造出很大的能量，足以把這個最小元素打破，就會形成更小的元素（歐洲核子研究組織CERN的大強子對撞機LHC正在加速運轉，或許可以完成這項任務）。如此一直這樣做下去，會不會出現數學上的無中生有？
我們是生活在三度空間之中，大家都會問宇宙所在的空間到底是有限還是無限的？若是有限的空間，那麼有限的空間之外又是什麼？一個永遠無法跨越的銅牆鐵壁嗎？可能嗎？若是宇宙是無限的那又是什麼情況？還是宇宙其實是有限的，只是它像圖三的莫比烏斯環（張瑞棋，2015）之類的3D模型，走了一段時間以後又會回到原來的地方（孤單旅行者，2017）？可是3D的莫比烏斯環有多大？之外的空間又是什麼？或許整個宇宙就是一種無限的概念。
圖3. 莫比烏斯環
▍ By David Benbennick, CC BY-SA 3.0, wikimedia commons.
李源順
臺北市立大學數學系教授
參考文獻
Weyl, H. & Pesic, P. （1930）. Levels of Infinity: Selected Writings on Mathematics and Philosophy（Dover Books on Mathematics）.
Zhao Zhong Chong（2021）。宇宙到底有邊嗎？財團法人國立自然科學博物館文教基金會。科普網路寫作平台。https://foundation.nmns.edu.tw/writing/hotnews2_detail.php？gid=11&id=1247
李肖梅（1993）：從微積分發展史看極限概念的演變（一）。科學教育月刊，第164期，pp.31-37。
林肯（2018）。夸克之內 別有洞天？科學人知識庫，932（12） https://sa.ylib.com/MagArticle.aspx？id=2112。
孤單旅行者（2017）。宇宙沒有邊際？怎麼可能，只是你不知道莫比烏斯環。每日頭條。https://kknews.cc/science/p66r3ge.html。
張瑞棋（2015）。無限循環的莫比烏斯環：莫比烏斯誕辰。科學史上的今天：11/17。泛科學，https://pansci.asia/archives/109598。
本文引用格式：李源順（2022）。漫談無限。科學研習，62（1），4-11。