文/張宮明
.png) 前言
前言
2011年的春天,筆者開設的數學專題研究課,迎來了新的一批高一學生,同時期筆者有多組學生在做不同議題的探究,在經過許多的文獻討論課程後,筆者的學生楊宗諺與陳玟旭對於參考文獻[4](盧崇文2009)的研究內容產生極大的興趣。其內容為:
「將一個樂隊放在第一象限,若要從周圍外一層攝影整個隊伍,則需要幾個攝影點才能將所有人拍攝到?」
針對此問題,筆者曾指導學生盧崇文(2009),經過一年的探討與研究,獲得了豐富的成果即參考文獻[4],筆者也將指導過程分享於去年的科學研習月刊(60卷2期)。這一次,筆者的另一組學生楊宗諺與陳玟旭延續學長的研究成果更進一步探究此問題,獲得更多新的結論,在2012年台灣國際科學展覽會上展現豐富的成果。
在探究初始,筆者要求楊&陳將參考文獻深入研究與探討。經過幾週的研讀與討論,我們定訂了初步的研究方向:
1.改良文獻[4]的不足之處,發展更優化的結果。
2.探究與文獻不同限制條件下的最小拍攝點集。
我們擬定一份研究計畫申請得到青少年科學人才培育計畫的補助,並獲得屏東教育大學傅東山教授的指導,這無疑是對我們的研究增添豐富的奧援。
就此,我們開啟一連串驚喜有趣的探究過程,筆者將引述楊&陳的研究報告(2012)與讀者分享。本文介紹的圖表與定理皆取自楊&陳的研究報告,也就是參考文獻[5](楊&陳,2012),筆者也會適當地增減與修正。特別提醒讀者,為了整篇文章的可讀性,本文也會提及參考文獻[4]中的某些定理,並且與楊&陳發展出的新結果比較其相異之處。
.png) 研究過程、方法與結果
研究過程、方法與結果
為了讓讀者更容易理解本文內容,筆者重新將題目內容敘述如下:
將一個樂隊放在坐標平面第一象限正整數格子點上,攝影師在原點、x軸、y軸正整數點上拍攝,則最少需要幾個拍攝點才能將所有人都拍攝完畢?
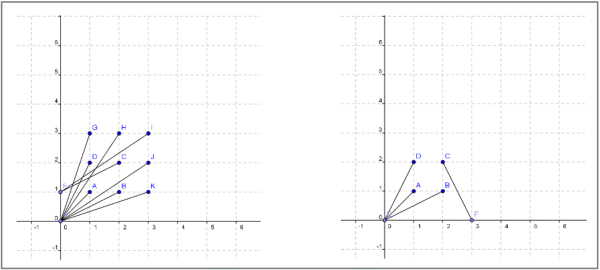 圖1.
圖1.
圖1是陣列3×3(左)和2×2(右)的拍攝情形,探究現有的參考文獻後發現:如果將攝影師的位置限制在原點與x軸(或y軸),造成所需的拍攝點較多。因此,筆者建議學生考慮攝影師的位置可以同時包含x軸與y軸上的點,深入探討上述問題。
接著,筆者指導學生將參考文獻[4]中常出現的名詞與定義做統整優化的工作,其內容如下。此部分的內容在參考文獻[4]中雖有述及,但所使用的定義與符號不夠清晰,而本文與其相異之處在於使用較有系統的文字符號來呈現。
一、優化名詞與定義
我們稱樂隊成員所在的點為目標點,稱攝影師所在的點為拍攝點。以符號N表示正整數所成的集合。對於m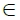 N,以符號V(m)表示下列目標點所成的集合
N,以符號V(m)表示下列目標點所成的集合
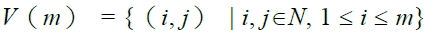 ,
,
※注意※ V(m) ⊂N×N是在第一象限內向y軸正向無限延伸的帶狀點集。
我們將拍攝點限制在原點及x軸,y軸上的正整數點。對於拍攝點a與目標點b而言,若線段ab上沒有其他目標點,則稱b點為a-可見(visible)。同理,對於拍攝點集A與目標點集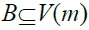 而言,若對每一點b
而言,若對每一點b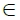 B存在一點a
B存在一點a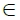 A使得b點為a-可見,則我們稱集合B為A-可見。
A使得b點為a-可見,則我們稱集合B為A-可見。
在充分探究參考文獻[4]的結果之後,我們想要發展文獻中沒有提及的領域或更好的結論。因此,筆者建議學生考慮在下列限制條件下,建構最小拍攝點集S,使得目標點集V(m)為S-可見的問題。
限制x軸上拍攝點落在集合{(i, 0) | 0 ≦ i ≦ m + 1}範圍內,拍攝點集S包含原點,並允許 y 軸上的正整數點。
若目標點集增加第二、三、四象限的帶狀點集,則最小拍攝點數與(一)之間關係為何?
將拍攝點集S限制在直線y = x上的正整數格子點,並允許y軸上的正整數點。
對於合作的團隊學生必須藉由互相討論與分工合作彼此磨合,指導老師需觀察團隊成員中的合作關係並給予適當的鼓勵與調整。楊&陳是相處多年的同學,彼此的合作非常有默契。在研究的初期就帶來先前文獻中沒有提到的新發現,其初步結果概述如下:
若以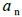 表示在原點拍攝n×n陣列時,所看不到的點的個數則
表示在原點拍攝n×n陣列時,所看不到的點的個數則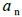 滿足下列遞迴關係式:
滿足下列遞迴關係式:
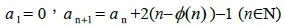 ,其中
,其中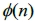 為尤拉函數。
為尤拉函數。
表1列出n=1到10的情形,詳細的證明會在後續的內容中提及。
表1.

這個觀察結果雖然只是一個小小的新發現,但卻是新苗長出來的重要時刻,因此,筆者以非常讚賞的態度鼓勵楊&陳,希望他們更進一步勇往直前探索未知。受到指導老師激勵的楊&陳更能感受發現新事物的喜悅與樂趣,因此更加熱情地探究此問題,研究就此順利展開。
二、基本性質
接下來,我們審視參考文獻[4]所列的基本性質(定理1、2,引理1、2),發現其不夠完備,經過重新論證之後,得到下列更優化的結果(引理1、2、3)。
將整個樂隊隊伍搬至坐標平面第一象限上拍攝,以數學的定義描述如下:
對於正整數m而言,考慮目標點集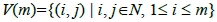 ,以符號
,以符號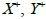 分別表示x軸,y軸上的正整數點所成的集合,即
分別表示x軸,y軸上的正整數點所成的集合,即


建構滿足下列條件的最小拍攝點集S使得V(m)為S-可見。
(1)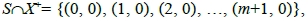 ,
,
(2) (0, 0)∈S,
(3)允許S包含部份y軸上的正整數點。
另外,假設攝影機並無拍攝角度之限制。
仔細觀察這些看不到點的現象,發現有下列基本性質(引理1至3):
.引理1. 以原點(0,0)為拍攝點,觀察目標點C(x, y),則C點為(0, 0)-可見若且唯若gcd(x, y)=1。
▍ 證明
設gcd(x, y) = d,x = ad,y = bd,則a, b∈N。令點A = (0, 0),點B =(a, b),則
AB直線的斜率為 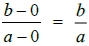
AC直線的斜率為 
所以線段AB的斜率等於線段AC的斜率,故兩直線重疊,若d = 1即B = C,此時C點為(0, 0)-可見。若d > 1,則B點在線段AC之上,此時C點不是(0, 0)-可見。
上述這些被其他點擋住而不能從原點看到的點或可稱為非原點可見。觀察這些點,由引理1,不難發現下列現象:
直線x = 2上非原點可見的點為{(2, 2n) | n∈N}
直線x = 3上非原點可見的點為{(3, 3n) | n∈N}
直線x = 6上非原點可見的點為{(6, 2n) | n∈N} ⋃{(6, 3n) | n∈N}。
依據以上觀察,考慮將拍攝點從原點移到x軸(或y軸)上的正整數點,得出以下性質。
.引理2. 設k, m為正整數,
(1)以點(k, 0)為拍攝點,觀察直線x = m上的目標點C(m, y),則C點是(k, 0)-可見若且唯若
gcd(m-k, y) = 1,
(2)以點(0, k)為拍攝點,觀察直線y = m上的目標點C(x, m),則C點是(0, k)-可見若且唯若
gcd(x, m-k) = 1。
▍ 證明
(1)經過平移,以(k, 0)為新原點,則C點的新坐標為(m-k, y)。由引理1得知C點是(k, 0)-可見若且唯若gcd(m-k, y) = 1。
(2)同理可證。
例如,如圖2所示,直線x = 2上非原點可見的目標點(2, 2n), n∈N與直線x = 3上非原點可見的目標點(3, 3n), n∈N可以利用y軸上的拍攝點(0, 5)去看。

圖 2. 由拍攝點(0, 0),(0, 5)去看目標點集V(3)
以下性質經常用在說明y軸拍攝點(0, r)對目標點的可見性。
引理3. 設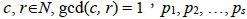 為c的質因數,
為c的質因數,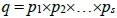 ,則對任意n∈N,gcd(c, qn-r) = 1恆成立。
,則對任意n∈N,gcd(c, qn-r) = 1恆成立。
▍ 證明
若存在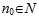 使得
使得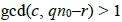 ,則存在c的質因數
,則存在c的質因數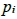 整除
整除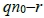 ,又因
,又因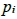 i整除q所以
i整除q所以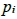 整除r,但這與假設gcd(c, r) = 1矛盾,因此對任意n∈N,gcd(c, qn-r) = 1。
整除r,但這與假設gcd(c, r) = 1矛盾,因此對任意n∈N,gcd(c, qn-r) = 1。
三、建構m < 10的最小拍攝點集
對於m < 10的情形,參考文獻[4]雖然有得到一些推論(推論1至9),但是並沒有論證最少拍攝點數,楊&陳在仔細研究後得出最少拍攝點數,如下列定理4所述。
以符號 |S| 表示集合S的元素個數,以符號σ(m)表示可觀看V(m)全體目標點所需的最小拍攝點數,即
σ(m) = min{|S| : V(m)為S-可見}
由上述引理,對於m < 10的情形可得出以下之結論。
.定理4. 設m為正整數,下列敘述成立。
(1)若 m = 1,則σ(m) = 1。
(2)若2 ≦ m ≦ 5,則σ(m) = 2。
(3)若6 ≦ m ≦ 9,則σ(m) = 3。
我們以各別討論的方式,試著找出最少的拍攝點。
(1) 當m = 1時,對於V(1) = {(1, n) | n∈N}而言,拍攝點僅需原點即可全部入鏡。
▍ 證明
對於n∈N,gcd(1, n) = 1,由引理1知目標點(1, n)均為原點可見。定理4敘述(1)成立。
當m > 1時,原點不足以看到全部V(m)的點,因此σ(m) ≧ 2。
(2) 當m = 2, 3, 4, 5時,對於V(m)而言,拍攝點集S = {(0, 0), (0, 7)}即能全部入鏡
▍ 證明
由敘述(1)知直線x = 1上的目標點均為原點可見。考慮直線x = 2, 3, 4, 5上那些原點看不到的點(2, 2n), (3, 3n), (4, 2n), (5, 5n), n∈N,這些點可從y軸上的拍攝點(0, 7)看到。理由是,若以點(0, 7)為新原點,這些點的新坐標分別為(2, 2n-7), (3, 3n-7), (4, 2n-7), (5, 5n-7)。由引理3知gcd(2, 2n-7) = gcd(3, 3n-7) = gcd(4, 2n-7) = gcd(5, 5n-7) = 1,由引理2之(2)得知這些點均為(0, 7)-可見。以上證明了定理4之敘述(2)。
(3) 當m > 5時,包含原點的拍攝點數至少為3,即σ(m) ≧3。
▍ 證明
考慮直線x = 6上非原點可見的目標點(6, 2n), (6, 3n),對於任意整數r都存在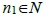 (或
(或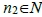 )存使得3整除
)存使得3整除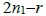 (或2整除
(或2整除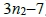 ),因此對於y軸上任意拍攝點(0, r),都存在直線x = 6上非原點可見的目標點
),因此對於y軸上任意拍攝點(0, r),都存在直線x = 6上非原點可見的目標點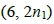 (或
(或 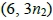 )為非(0, r)-可見。
)為非(0, r)-可見。
很明顯,對於x軸上的一拍攝點(i, 0),i∈{1,2,3,4,5,6,7},不足以看到全部V(6)的非原點可見的目標點。
(4) 當m = 6, 7, 8, 9時,對於V(6)而言,拍攝點集S = {(0, 0), (7, 0), (0, 11)}即能全部入鏡。
▍ 證明
考慮非原點可見且非(7, 0)-可見的目標點(2, 10n), (3, 6n), (4, 6n), (5, 10n), n∈N。這些點將可從y軸上的拍攝點(0, 11)看到。理由是,若以點(0, 11)為新原點,這些點的新座標分別為(2, 10n-11), (3, 6n-11), (4, 6n-11), (5, 10n-11)。由引理3知gcd(2, 10n-11) = gcd(3, 6n-11) = gcd(4, 6n-11) = gcd(5, 10n-11) = 1,由引理2之(2)得知這些點均為(0, 11)-可見,故V(6)為S-可見。
考慮直線x = 7, 8, 9上的目標點,很明顯,那些非原點可見的點均為(0,11)-可見。
以上證明了定理4之敘述(3)。
※附註※ 上述V(m)的最小拍攝點集不是唯一的,例如,對於V(m), m = 6, 7, 8, 9, 的拍攝點集S也可以取S = {(0, 0), (5, 0), (0, 11)}。
四、建構m ≧ 10的最小拍攝點集
當m ≧ 10時,我們以參考文獻[4]的定理3為基礎,並加以改良,提出覆蓋點集的新概念,對於目標點集V(m)我們提出一個完整建構拍攝點集S的方法即本文中的定理5,並且證明之。這個方法的步驟有些複雜,其內容如下所述,請讀者有耐心地閱讀。
將目標點依其所在的直線x = c加以分類,我們將集合{1, 2, ..., m}分割成三個子集
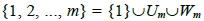 ,
,
其中 是那些質數冪所成的集合,而
是那些質數冪所成的集合,而 是那些剩下的數所成的集合,換言之
是那些剩下的數所成的集合,換言之
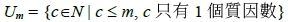 ,
,
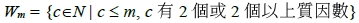 。
。
例如,當m = 10時,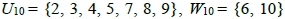 ,當m = 15時
,當m = 15時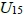 = {2, 3, 4, 5, 7, 8, 9, 11, 13},
= {2, 3, 4, 5, 7, 8, 9, 11, 13}, 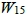 = {6, 10, 12, 14, 15}。
= {6, 10, 12, 14, 15}。
若 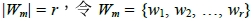 。對於1 ≦ i ≦ r,設
。對於1 ≦ i ≦ r,設 個質因數,並令這些質因數為
個質因數,並令這些質因數為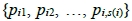 ,考慮
,考慮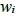 所衍生型如
所衍生型如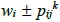 的正整數類型,定義集合
的正整數類型,定義集合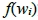 如下,其中k為任意非負整數
如下,其中k為任意非負整數
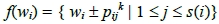 ,
,
並定義F(m)為所有這些類型所成的集合,即
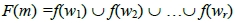 。
。
若正整數t可以表示成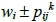 的形式,則稱t涵蓋
的形式,則稱t涵蓋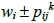 類型。考慮正整數集T ⊂ {1, …, m+1},若對每一類型
類型。考慮正整數集T ⊂ {1, …, m+1},若對每一類型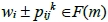 ,存在t∈T使得t涵蓋
,存在t∈T使得t涵蓋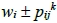 類型,則稱T為F(m)-覆蓋。我們的目的就是利用F(m)-覆蓋建構x軸上的拍攝點集。
類型,則稱T為F(m)-覆蓋。我們的目的就是利用F(m)-覆蓋建構x軸上的拍攝點集。
例如,當m = 10時,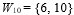 ,其中6的質因數為{2, 3},10的質因數為{2, 5},則6與10分別衍生正整數類型
,其中6的質因數為{2, 3},10的質因數為{2, 5},則6與10分別衍生正整數類型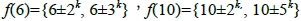 ,因此
,因此
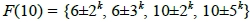 。
。
當k = 0時,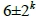 = {7, 5},
= {7, 5}, 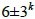 = {7, 5},
= {7, 5}, 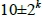 = {11, 9},
= {11, 9}, 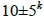 = {11, 9},知7與5涵蓋
= {11, 9},知7與5涵蓋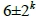 類型與
類型與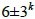 類型,11與9涵蓋
類型,11與9涵蓋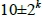 與
與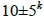 類型,因此構成F(10)-覆蓋的集合T有{5, 9}, {5, 11}, {7, 9}, {7, 11};當k = 1時,
類型,因此構成F(10)-覆蓋的集合T有{5, 9}, {5, 11}, {7, 9}, {7, 11};當k = 1時,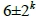 = {8, 4},
= {8, 4}, 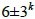 = {9, 3},
= {9, 3}, 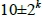 = {12, 8} (因12> m+1=11,可以捨去),
= {12, 8} (因12> m+1=11,可以捨去), 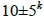 = {15, 5}(因15> m+1=1,可以捨去),知8涵蓋
= {15, 5}(因15> m+1=1,可以捨去),知8涵蓋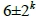 類型與
類型與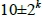 類型,依此類推;當k = 2時,
類型,依此類推;當k = 2時,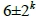 = {10, 2},
= {10, 2}, 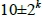 = {14, 6}。我們將結果整理成下表2,以利說明:
= {14, 6}。我們將結果整理成下表2,以利說明:
表2.

由表得知,構成F(10)-覆蓋的集合T有{5, 9}, {5, 11}, {7, 9}, {7, 11}, {5, 8}, {8, 9}, {3,9,11}, …,等,但{7, 8}不是一個F(10)-覆蓋,因為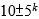 類型不能被7與8所涵蓋。
類型不能被7與8所涵蓋。
注意,對於m ≧ 10,任何一個F(m)-覆蓋T至少包含2個元素。
以下,對於目標點集V(m),我們利用F(m)-覆蓋建構拍攝點集S使得V(m)為S-可見。
.定理5. 設正整數m ≧ 10,T ⊂ {1, …, m+1}為一個F(m)-覆蓋,r為大於m的最小質數,對於目標點集V(m) = {(i, j) | i, j∈N, 1≦ j ≦ m},建構拍攝點集S = {(0, 0), (0, r)} ⋃ {(t, 0) | t∈T},則V(m)為S-可見。
▍ 證明
為了證明V(m)為S-可見,我們將目標點依其所在的直線x = c分類,因此將集合{1, 2, ..., m}分割成上述三個子集{1},  ,
,  ,分別討論如下:
,分別討論如下:
(1) 當c = 1時,很明顯,直線x = 1上所有目標點均為原點可見。
(2) 當c∈ 時,c只有1個質因數p,考慮直線x = c上那些非原點可見的目標點(c, pn), n∈N,由引理3知對於任意n∈N, gcd(c, pn-r) = gcd(c, r) = 1,因此由引理2之(2)得知這些目標點
時,c只有1個質因數p,考慮直線x = c上那些非原點可見的目標點(c, pn), n∈N,由引理3知對於任意n∈N, gcd(c, pn-r) = gcd(c, r) = 1,因此由引理2之(2)得知這些目標點
(c, pn)都可被y軸上的拍攝點(0, r)所看見。
(3) 當c∈ 時,c有2個或2個以上質因數,令這些質因數為
時,c有2個或2個以上質因數,令這些質因數為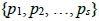 。因T是一個F(m)-覆蓋,故存在
。因T是一個F(m)-覆蓋,故存在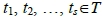 使得
使得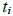 涵蓋
涵蓋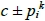 類型 (1 ≦ i ≦ s)。
類型 (1 ≦ i ≦ s)。
對於相異的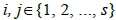 ,存在a, b∈N使得
,存在a, b∈N使得 。由引理3知對於任意n∈N,當n不是
。由引理3知對於任意n∈N,當n不是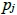 的倍數時,
的倍數時,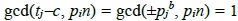 。同樣的,當n不是
。同樣的,當n不是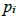 的倍數時,
的倍數時,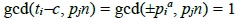 。
。
考慮直線x = c上那些非原點可見的目標點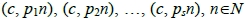 ,拍攝點
,拍攝點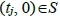 可看見目標點
可看見目標點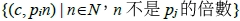 ,但看不見目標點
,但看不見目標點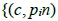 | n∈N,n是
| n∈N,n是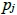 的倍數}。同樣的,拍攝點
的倍數}。同樣的,拍攝點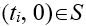 可看見目標點
可看見目標點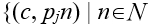 ,n是
,n是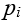 的倍數,但看不見目標點
的倍數,但看不見目標點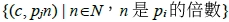 。令
。令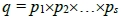 ,則直線x = c上只剩下目標點(c, qn), n∈N不能被拍攝點
,則直線x = c上只剩下目標點(c, qn), n∈N不能被拍攝點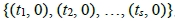 所看見,而這些目標點(c, qn) 可被y軸上的拍攝點(0, r)所看見,理由是gcd(c, qn-r) = gcd(c, r) = 1,因此我們證明了V(m)為S-可見。
所看見,而這些目標點(c, qn) 可被y軸上的拍攝點(0, r)所看見,理由是gcd(c, qn-r) = gcd(c, r) = 1,因此我們證明了V(m)為S-可見。
例如,當m = 10時,
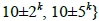 。對於目標點集V(10)建構拍攝點集S = {(0, 0), (0, 11), (7, 0), (9, 0)}使得V(10)為S-可見,茲說明如下。
。對於目標點集V(10)建構拍攝點集S = {(0, 0), (0, 11), (7, 0), (9, 0)}使得V(10)為S-可見,茲說明如下。
考慮直線x = c上的目標點,當c = 1時,顯然直線x = 1上的目標點均為原點可見。
當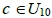 時,非原點可見的的目標點有(2, 2n), (3, 3n), (4, 2n), (5, 5n), (7, 7n), (8, 2n), (9, 3n), n∈N,這些點都是(0, 11)-可見。
時,非原點可見的的目標點有(2, 2n), (3, 3n), (4, 2n), (5, 5n), (7, 7n), (8, 2n), (9, 3n), n∈N,這些點都是(0, 11)-可見。
當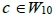 時,非原點可見的的目標點有(6, 2n), (6, 3n), (10, 2n), (10, 5n), n∈N。
時,非原點可見的的目標點有(6, 2n), (6, 3n), (10, 2n), (10, 5n), n∈N。
若取F(10)-覆蓋T = {7, 9}知拍攝點(7, 0)可看見直線x = 6上的目標點,拍攝點(9, 0)可看見直線x = 10上的目標點,因此建構拍攝點集S = {(0, 0), (7, 0), (9, 0), (0, 11)}可使V(10)為S-可見。
若取F(10)-覆蓋T = {5, 8}知直線x = 6上的目標點可被拍攝點(5, 0)可看見,但直線x = 10上的部份目標點(10, 10n) , n∈N被不能被拍攝點(5, 0)及(8, 0)可看見,而這些點均為(0, 11)-可見,因此建構拍攝點集S = {(0, 0), (5, 0), (8, 0), (0, 11)}亦可使V(10)為S-可見。
由定理5,要建構V(m)的最小拍攝點集S就要搜尋最小的F(m)-覆蓋,以符號κ(m)表示最小F(m)-覆蓋的點數,即
κ(m) = min{|T| : T為F(m)-覆蓋},
則我們有以下結果。
.定理6. 若m為正整數,則σ(m) ≦ κ(m) + 2。
此結果與參考文獻[4]中定理5的結果不同之處在於我們指出最少拍攝點數的上界,並且繼續推演出新的發展如下。
在研究過程中發現我們觀察到一個現象,當m為質數時,V(m)與V(m-1)所需的拍攝點個數相同,經過思考之後知道,因為m是質數,不會產生新的類型,換言之F(m) = F(m-1),我們得出下列推論。
.推論7. 若m為質數,則 κ(m) = κ(m - 1)。
當數字m越大時,構成F(m)-覆蓋的集合也越多,此時需要數學軟體輔助加以運算。下列表3是我們目前找出來最小覆蓋的點數:

我們試著使用迴歸直線去預測接下來的最小覆蓋的點數κ(m),以1≦m≦100計算資料得出迴歸直線為
κ(m) = (2028585m + 2906864)/8329699
其相關係數為0.994141。
因為在參考文獻[4]的定理6有提及π函數與拍攝點數的關係,所以筆者請楊&陳研究他們的相關性,並獲得新的進展如下猜想8。
下列圖3為κ(m)與π函數的對照圖,其中π函數定義π(m)為小於或等於m的質數個數。經過觀察,我們發現κ(m)與π(m)函數有高度相關性,至於他們之間的關係為何?目前尚無確定的結論。

圖 3. κ(m)與π函數的對照圖
.猜想8. 若m為正整數,則 κ(m) + 2 ≦ π(m) 。
與先前文獻之結果比較,參考文獻[4]探討對於目標點集V(m),拍攝點限制在x軸上點集合{(i, 0) | 1 ≦ i ≦ m + 1},建構V(m)-可見的最小拍攝點集S,得到結論是當m是4的倍數時,|S| =m/2,當m不是4的倍數時,|S| =[m/2] + 1,其中符號[x]表示高斯函數。

如下圖4,將這個函數與我們所做(允許y軸上拍攝點)的結果κ(m) + 2比較,我們發現所需的拍攝點數大幅降低。

圖 4. κ(m) + 2與f(m)對照圖
我們在研究過程中,我們曾考慮以原點為拍攝點,目標點集為m×m方陣
M(m) ={(i, j) | i, j∈N, 1≦ i, j ≦ m},
我們發現一個有趣特殊性質,以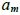 表示M(m)中原點所看不到的目標點個數,下表4列出我們觀察到
表示M(m)中原點所看不到的目標點個數,下表4列出我們觀察到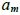 的初始值(1 ≦ m ≦ 10)
的初始值(1 ≦ m ≦ 10)
表4.

我們得到以下結果。
.定理9. 以下等式成立,其中符號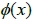 表示尤拉函數,
表示尤拉函數,

▍ 證明
比較M(k)與M(k-1),目標點多出2k-1個點,分布在直線x = κ上與直線y = κ上,其中原點可見的目標點在直線x = κ上有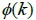 個,在直線y = κ上有
個,在直線y = κ上有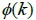 個,因此數列
個,因此數列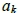 滿足遞迴關係式
滿足遞迴關係式

上述等式做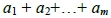 ,即可得證。
,即可得證。
另外,考慮以點(1, 1)∈M(m)為拍攝點,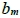 表示M(m)中(1, 1)點所看不到的目標點個數(包含(1, 1)點本身),有以下結果。
表示M(m)中(1, 1)點所看不到的目標點個數(包含(1, 1)點本身),有以下結果。
.定理10. 以下等式成立,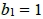 ,當m ≧ 2時,
,當m ≧ 2時,

▍ 證明
目標點M(m)可分成直線x =1,直線y = 1,與(m-1)×(m-1)方陣,其中在直線x = 1,y = 1上分別有m-2個(1, 1)點所看不到的目標點,加上(1, 1)點本身,共2m-3個點。以(1, 1)點去看這個(m-1)×(m-1)方陣相當於以原點去看M(m-1),有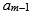 看不到的目標點,因此,
看不到的目標點,因此,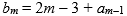 ,由定理9,將
,由定理9,將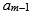 代入得證。
代入得證。
承上,很明顯,若將拍攝點移到其他三個角落的點(m, 1), (1, m), (m, m)∈M(m),則會有相同點數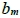 看不到的目標點。
看不到的目標點。
五、建構四個象限目標點集的最小拍攝點集
以下我們考慮增加第四象限的目標點,以符號A(m)表示下列目標點所成的集合
A(m) = V(m) ⋃ {(i, -j) | i, j∈N, 1 ≦ j ≦ m},
拍攝點仍限制在原點及x軸,y軸上的正整數點。我們發現雖然目標點增為加一倍,但所需的點拍攝點並未增加,即只需 κ(m) + 2個拍攝點就可將A(m)全部入鏡,我們得到以下定理:
. 定理11. 設m為正整數,T ⊂ {1, …, m+1}為一個F(m)-覆蓋,r為大於m的最小質數,對於目標點集A(m) = {(i, j), (i, -j) | i, j∈N, 1≦ j ≦ m},建構拍攝點集
S = {(0, 0), (0, r)} ⋃ {(t, 0) | t∈T},則A(m)為S-可見。
▍ 證明
設T是一個F(m)-覆蓋,建構拍攝點集S ={(0, 0), (0, r)}⋃{(t, 0) | t∈T},則V(m)是S-可見,對於直線x = c上的目標點,若目標點(c, j) ∈V(m)可被x軸上的拍攝點(t, 0) ∈S看見,則gcd(c-t, j) = 1= gcd(c-t, -j),因此目標點(c, -j) ∈A(m)也可被拍攝點(t, 0)看見。至於那些不能被x軸上拍攝點看到的點(c, qn), n ∈N,其中q為c的質因數乘積,則由y軸上的拍攝點(0, r) 負責去看,因gcd(c, -qn-r) = 1 =gcd(c, qn-r), n∈N,因此目標點(c, -qn) ∈A(m)也可被拍攝點(0, r)看見,故A(m)也S-可見。
下圖5為利用拍攝點{(0, 0), (0, 5)}去看目標點A(3)。

圖5. 由拍攝點(0, 0),(0, 5)去看目標點集A(3)
考慮將目標點A(m)沿著y軸翻轉以增加第二及第三象限的目標點,以符號B(m)表示下列目標點所成的集合
B(m) = {(-i, j) | (i, j)∈A(m)},
拍攝點仍限制在原點及x軸,y軸上的正整數點,我們得到以下定理:
. 定理12. 設m為正整數,對於目標點集A(m)⋃B(m)的最小拍攝點數σ(m),有
σ(m) ≦ min{2κ(m) + 2, κ(2m+1) + 2}。
▍ 證明
設T是一個F(m)-覆蓋,建構拍攝點集S ={(0, 0), (0, r)} ⋃{(t, 0) | t∈T}⋃{(-t, 0) | t∈T},由定理10知,目標點集A(m)可被拍攝點{(0, 0), (0, r)} ⋃{(t, 0) | t∈T}所看見,而目標點集B(m)可被拍攝點{(0, 0), (0, r)} ⋃{(-t, 0) | t∈T}所看見,所以A(m) ⋃B(m)是S-可見,因此σ(m) ≦ 2κ(m) + 2。另外,考慮將y軸平移到直線x = -m -1上,相當於整個目標點落在A(2m+1)之內,而x軸上所需的攝點集可以由F(2m+1)-覆蓋建構得到,因此σ(m) ≦ κ(2m+1) + 2。
六、建構在直線y = x及y軸上的最小拍攝點集
我們又回到第一象限的目標點集V(m),這次變更拍攝點的限制,拍攝點限制在原點,直線y = x上正整數點及y軸上正整數點,其結果如下:
.定理13. 設m為正整數,T ⊂ {1, …, m+1}為一個F(m)-覆蓋,r為大於m的最小質數,對於目標點集V(m) = {(i, j) | i, j∈N, 1 ≦ j ≦ m},建構拍攝點集S = {(0, 0), (0, r)} ⋃ {(t, t) | t∈T},則V(m)為S-可見。
▍ 證明
將目標點依其所在的直線x = c分類,因此將集合{1, 2, ..., m}分割成上述三個子集{1},

,由定理5的證明知,當c = 1或c∈

時,直線x = c上所有目標點都可被{(0, 0), (0, r)}所看見,現在討論c∈

時的情形如下:
令

為c的質因數(s ≧ 2)。因T是一個F(m)-覆蓋,故存在
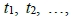

使得ti涵蓋

類型 (1 <= i <= s)。對於相異的i, j∈{1, 2, ..., s},存在a, b∈N使得

。由引理3知對於任意n∈N,當n不是pj的倍數時,

。同樣的,當n不是pi的倍數時,
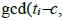

。
考慮直線x = c上那些非原點可見的目標點

,拍攝點

可看見目標點

,但看不見目標點


。同樣的,拍攝點

可看見目標點

不是

的倍數},但看不見目標點

。令

,則直線x = c上只剩下目標點(c, qn), n∈N不能被拍攝點

所看見,而這些目標點(c, qn) 可被y軸上的拍攝點(0, r)所看見,理由是gcd(c, qn-r) = gcd(c, r) = 1,因此我們證明了V(m)為S-可見。
下圖6為利用拍攝點{(0, 0), (5, 5)}去看目標點V(3)。
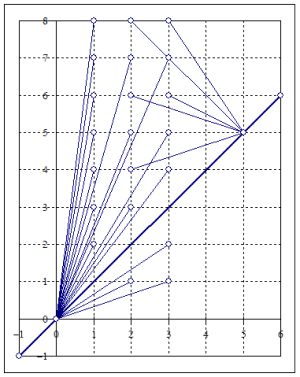 圖 6. 由拍攝點(0, 0),(5, 5)去看目標點集V(3)
圖 6. 由拍攝點(0, 0),(5, 5)去看目標點集V(3)
.png) 結論
結論
在參考文獻[4]的基礎上,我們優化改良文獻的結果並發展出更多文獻中未曾提及的新結論,我們將此部分綜合整理如下。
設m為正整數,對於目標點集V(m),拍攝點包含原點並限制在以及x軸,y軸正向的整數點上而且x軸上的拍攝點不可以超過(m+1,0),最小拍攝點數σ(m)有下列結果:
若 m = 1,則σ(m) = 1。
若2 ≦ m ≦ 5,則σ(m) = 2。
若6 ≦ m ≦ 9,則σ(m) = 3。
若m ≧ 10,我們提出F(m)-覆蓋的想法去建構x軸上的拍攝點,得到σ(m)好的上界κ(m) + 2,其中κ(m)是最小F(m)-覆蓋點數,我們也認為κ(m) + 2不會超過m以內的質數個數π(m)。
增加第四象限的目標點數不會造成最小拍攝點數增加。
若拍攝點在第一、二、三和第四象限,則只需2κ(m) + 2個拍攝點。
對於目標點集V(m),拍攝點包含原點並限制在直線y = x以及y軸正向的整數點上,則只需κ(m) + 2個拍攝點。
.png) 給讀者的展望
給讀者的展望
對於本研究還可繼續發展的部分,我們提出下列幾點供有興趣的讀者參考。
由於κ(m)是從許多F(m)-覆蓋中找出最小覆蓋的點數,我們嘗試找一個好的估計,例如π函數。讀者也可以就此估計做更深入的研究。
我們找觀測點方式分成許多小細節和步驟,因此我們將步驟與限制輸入電腦運作時會有書寫程式和運作上的問題。希望有興趣的讀者可以試著將它簡化或者探究另一套更快更準的找法,並利用電腦程式的幫助更快找出結果,進一步去探究拍攝點和m之間的關係。
建議讀者進一步嘗試拍攝點不限制在x軸,y軸或直線y = x上,而以其他點作為拍攝點,希望可以發展出拍攝點擺放在特殊的直線或曲線上,做出相關的成果。
事實上,我們可以試著推廣到三度空間,對於空間中的原點可見的目標點有類似引理1的性質,以原點(0, 0, 0)為拍攝點,觀察目標點C(x, y, z),則C點為(0, 0, 0)-可見若且唯若gcd(x, y, z)=1。另外,空間中的可見點仍然保有平面可見點的性質,即在平面上,原點可見的目標點(x, y)其x, y坐標互質,那麼即使到了高維度空間,只要該點的x, y坐標互質,無論其他軸向的坐標為何,該點即可被原點看到。然而,在空間中拍攝點集的選取可能有更多變化的選項,有興趣的讀者可以進一步深入探究。