前言

筆者長期帶領高中生從事專題研究進而形成科展作品，研究與討論的過程非常有樂趣；就是這股樂趣，讓筆者能繼續不斷與學生探討與研究。

本文分享的作品「單淘汰制賽程分析」是由王啟樺同學研究，筆者指導的專題研究成果，在2010年獲得台灣國際科學展覽會大會二等獎，美國2010年國際科技展覽會(ISEF)大會三等獎的殊榮。雖然已相隔10年才與讀者分享，但回想起研究過程中的點點滴滴仍然歷歷在目。

在各種比賽的制度中，單敗淘汰賽是常見的賽程，這種賽制很容易理解，只要敗一場就淘汰，而且每一場一定要分出勝負，沒有不分勝負的和局。圖1與圖2分別為4人與8人的賽程表。本文介紹的圖表與定理皆取自啟樺的研究報告。


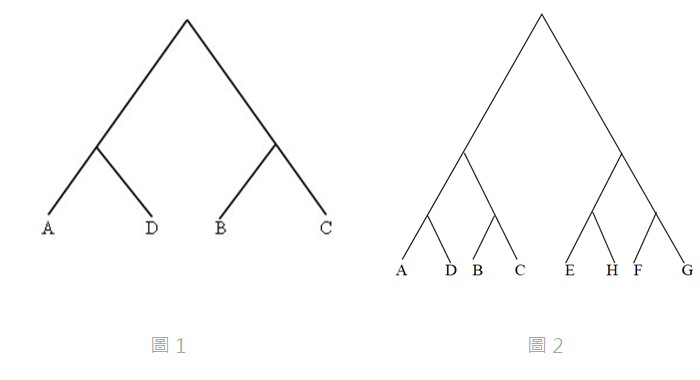圖1. 4人單敗淘汰賽程、圖2. 8人單敗淘汰賽程

在筆者的專題研究課程中引導學生在網路上搜尋有興趣的研究主題，啟樺在台灣國際科展的歷屆作品中發現了于小涵同學於2006台灣國際科學展覽會的作品「輸贏一線間--淘汰賽的相關探討」，在于同學的作品中得知包含8人的賽程表中，藉由賽程的安排，使得次強選手獲得冠軍的機率大於最強選手的可能性存在。啟樺對這個主題有高度的興趣，因此，我建議他，先把于同學的作品從頭到尾徹徹底底地推演一遍，不僅要讀懂作者的思路與推演方法，也要提出自己的想法。啟樺真的準備一本筆記扎扎實實地將整個作品研究了幾遍，並且將研讀心得於專題研究課中報告與討論，當然，這過程是非常耗時費力的，但也因此，啟樺熟透了這個主題。

 關鍵提問

一開始，啟樺推演出許多有趣的結果，並將淘汰賽研究結果應用在網路的票選活動上做數學建模與獲勝機率的預測，得到很多豐富有趣的結論。於此同時，透過網路，搜尋到了黃光明教授發表在數學傳播的〈淘汰賽〉一文，進一步認識了淘汰賽於數學上的表達方式。經過深入的研讀，在其中一堂專題研究課中，啟樺向筆者提出一個問題：「在未進行任何賽程之前，如何衡量各選手對A選手的威脅？」這是一個非常關鍵的提問，讓整個研究有了探索分析的標的物，不再只是一般的算術問題。接下來，筆者將從啟樺豐富的研究成果中節錄部分內容與讀者分享其研究與探索的過程。

 研究過程與方法

為了使在單淘汰賽中獲勝的機率問題得以討論，在此訂定兩個定義：

定義一：每名選手皆有其自身的實力，若將選手命名為Ａ、Ｂ、Ｃ、Ｄ……，則各選手對應之實力依序為 a、b、c、d……。

定義二：令 PAB 為選手 A 與選手 B 比賽時，選手 A 勝出的機率，並規定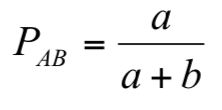

例如：若選手 A 與選手 B 的實力分別為3與2，則選手 A 勝出的機率為

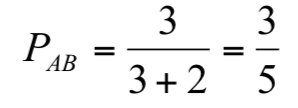
直觀上我們認為「只要敵人的實力增強，對我的威脅就會增加」，而在賽程中，亦即意味著 「任何敵人實力增加，我的勝率就會下降」。現在，我們想要證明這個直觀。

一、包含4名選手的賽程

如圖 1 是一個包含 4 名選手的賽程表。就選手 A 而言，第 1 場賽程的對手必然是選手 D，晉級所受到的威脅只需比較選手D的實力即可判斷。所以第 1 場賽程中，由定義可知A選手獲勝的機率為



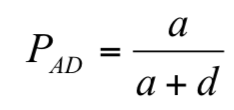
由上式可直接看出當D選手實力提升時，A選手的勝率就下降，這證明了在第1場賽程中「只要敵人的實力增強，對我的威脅就會增加」。

然而，第 2 場賽程可能遇上的對手為選手 B 或選手 C。在未進行任何賽程之前，這兩名選手對我的威脅有多大呢？是否還是符合「只要敵人的實力增強，對我的威脅就會增加」與「任何敵人實力增加，我的勝率就會下降」，這兩種直觀呢？這是我們想要探究的目的之一。

因為第2場賽程的選手是不確定的，一開始啟樺不知道如何探討這個議題，筆者建議把4人賽程表畫在黑板上，如圖1。把問題寫在黑板上是筆者專題研究課最常做的事。望著賽程表，啟樺和筆者有如下的一段關鍵對話。

啟樺問筆者：「我雖然可以算出這賽程表中，A獲得冠軍的機率(如定理1中的(1)式)，但是，我如何推算B或C選手實力的變化對A獲得冠軍之機率的影響呢？」

筆者回答：「因為A在第二場比賽面對的選手不確定是B或C，對於不確定的事物，我們通常習慣把它假設為X。」

就這樣我們在黑板的賽程表中畫上了X，如圖3，

筆者問啟樺：「如果現在用X來取代B和C選手，那A獲得冠軍的機率是如何表示呢？」

啟樺在黑板上將算式寫出來，如(2)式，再來利用兩式中，A選手的冠軍機率相等，就可推得定理1中X選手的實力是b和c的函數。如此，b、c的變化對x的影響就可以討論了。

換句話說，我們嘗試建立一名假想選手 X，藉由將選手 B 與選手 C 替換為假想選手 X，我們可以得到簡化後選手 A 的賽程表如圖 3 表示。則我們得到關鍵的定理1。


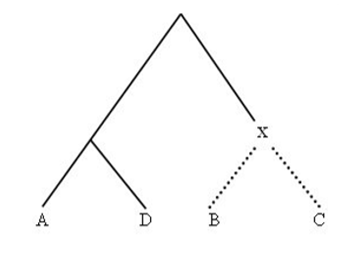
圖3

定理 1 相對於選手 A 的假想選手 X 之實力為 x，則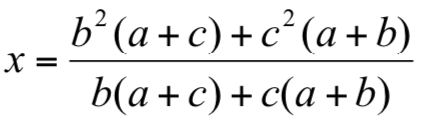

證明: 由圖 3 與圖 4 可分別得到選手 A 的勝率如(1)、(2)：


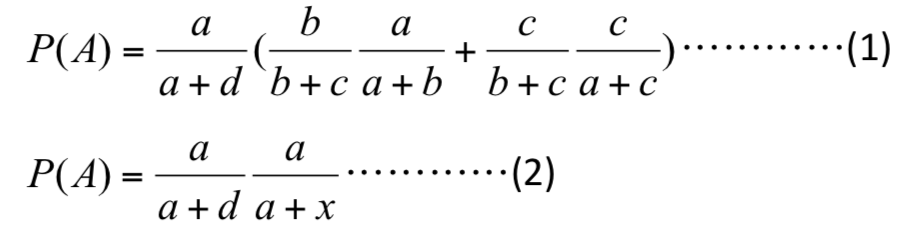
同一張賽程表中，因為選手 A 贏得比賽的機率相同，因此由(1)、(2)相等可得：

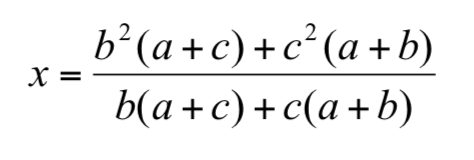
定理1是一個很有趣的關鍵結果，從定理1可以看出當a與c固定時，x是b的有理函數，因此我建議啟樺可以探討b的變化對x的影響是如何？也就是探討B選手的實力變化，對假想選手X的實力會造成何種變化？

換言之，藉由假想選手 X，我們可以判斷在未進行任何賽程之前，第 2 場賽程可能遇上的選手對A所造成的威脅。接下來，透過例子，讓我們更了解「假想選手」。

在圖 1 中，為了方便比較，我們先假設選手 C 的實力 c = a，選手 D 的實力 d = a /10，觀察選手 B 的實力 b = a / 5、a / 4、a / 3、a / 2、a 時，假想選手 X 的實力 x 之變化。結果如表1。

表1. 假想選手 X 的實力 x 之變化


由表1我們可以知道，當選手 C 的實力 c = a，選手 B 的實力 b = a / 2 時，對於選手 A 而言， 第二場賽程遇到的對手，其實力相當於 4/5 a。透過「假想選手」，我們能夠了解第二場賽程所可能遇上的對手對自己所造成的威脅。

眼尖的讀者，從上面的例子或許已經發現：當b遞增時，假想選手X實力的變化一開始是遞減，但隨後又變成遞增，這是個非常有趣的現象，因此，我建議啟樺探究這種變化的原因。換句話說，就是研究函數 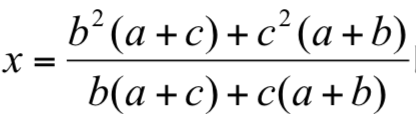的遞增與遞減行為。因為此函數是有理函數，所以筆者建議啟樺研讀相關的微積分書籍，了解如何判斷函數的遞增與遞減行為。  

二、威脅門檻 (Threshold of Threat)

定義三：令 Pn(A)為選手 A 晉升至上方第 n 節點的機率，即連續贏得n場比賽的機率。

由定理 1，我們可以判斷在未進行任何賽程之前，第二場賽程可能遇上的選手對A造成的威脅。參照圖 3 選手 A 的賽程表，第二場將遇上的對手為假想選手 X。依照直觀，則 「選手 B 的實力增加，將造成假想選手X 的實力增加而使選手 A的勝率下降」。因此， 我們便猜想假想選手X的實力 x為選手 B 的實力 b 之嚴格遞增函數。但是經過探究後，我們得到了意想不到的結果。

定理 2 存在一威脅門檻 b0，若 B 選手之實力 b> b0，則 b 增加將使 P2(A)下降；若 B 選手之實力 b< b0，則 b 增加將使 P2(A)上升。其中:

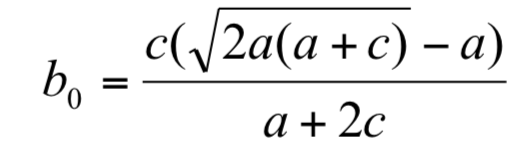
證明：
令 x 為函數 f(b)，使 x = f(b)。檢驗 f(b)是否為 b 之嚴格遞增函數。

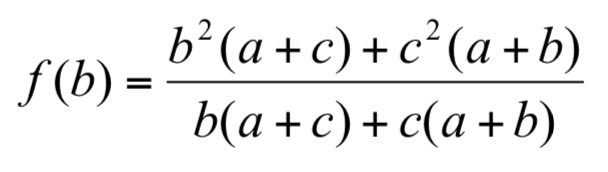
作 f(b)之一次導函數：

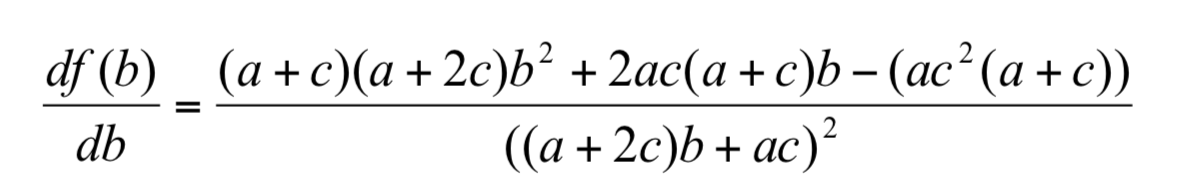
其一次導函數的分母恆正，分子則為 b 之二次函數，領導係數恆正且由判別式大於 0 知其圖形是與橫軸交於兩點且開口向上的拋物線。以圖形頂點將拋物線分為左右兩支，則左支呈嚴格遞減函數，右支為嚴格遞增函數。令其一次導函數之分子為 g(b)，使得

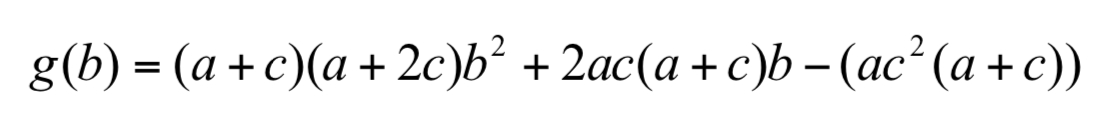
令 g(b)為 0，解出 b 之二實根，得一正根一負根：

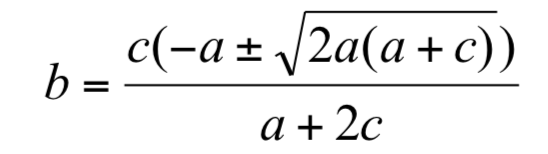
取其正實根，並命名為 b0，使得

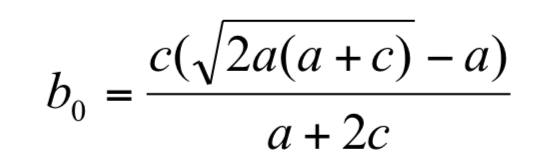
將 g(b)之函數圖形繪出，如圖 4，則當 b> b0， g(b)>0， f(b)為嚴格遞增函數，此時b 上升將使 x 上升而使 P(A)下降。當 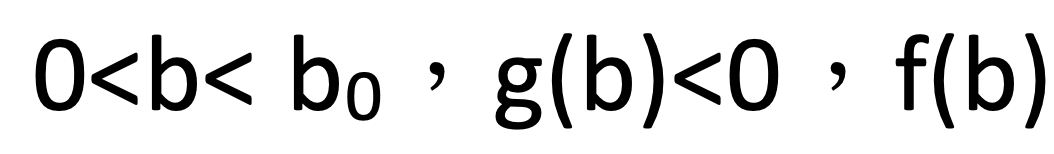為嚴格遞減函數，此時 b 上升將使x下降而使 P(A)上升。


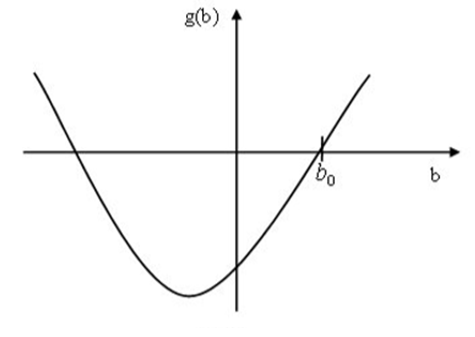
圖4. g(b)之函數圖形

定理 2 是一個十分耐人尋味的結果，代表 B 選手的實力 b 有一個門檻 b0，當 b>b0 時，B 選手的實力增加，對 A 選手才會造成威脅(即使 P(A)下降)；而當 b<b0 時，B 選手實力增加卻對 A 選手之勝率 P(A)有提升的作用。不但否定了直觀上「只要敵人的實力增強，對我的威脅就會增加」的迷思，甚至證明了列寧於統一戰線理論中所提出的「聯合次要敵人，打擊主要敵人」策略的理論基礎。即培養將來可能的對手使其實力增加，竟然有可能增加自己未來的勝率，這真是非常有趣的結果。

現在，讓我們看一個例子。在圖 1 中，我們令選手 C 的實力 c = a，選手 D 的實力 d = a /10，則選手 B 的威脅門檻為 a / 3。我們讓選手 B 的實力 b 由 a / 5 遞增至 a，觀察選手 B 的實力與選手 A 的勝率之關係。結果如表2:

表2. 選手 B 的實力與選手 A 的勝率之關係


有趣地，我們可以發現，在選手 B 的實力 b 小於威脅門檻 a/3 時，其實力增加亦會增加選手 A 的勝率；而當選手 B 的實力 b 大於威脅門檻 a/3 時，其實力增加便開始讓選手 A 的勝率下降了。

此外，啟樺注意到賽程有時後會安排種子選手，假設一包含種子選手的賽程表如圖5，若選手 B 為種子選手，則c=0，因此其威脅門檻 b0=0。因此，我們有以下推論。

推論1 設一包含種子選手的賽程表如圖5，若選手 B 為種子選手，則其威脅門檻 b0=0。


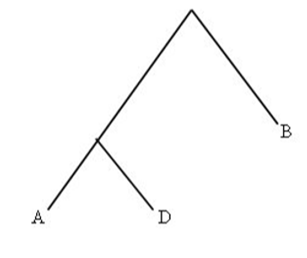
圖5. 包含種子選手的賽程

三、包含 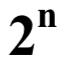名選手的賽程

有了以上的結果，筆者建議啟樺繼續探討包含8名選手的賽程，為了探討更多名選手的賽程，我們有以下的定義：
定義四：令 Xn為選手將晉升至第 n 節點時所遇到的假想選手。

（一）假想選手 Xn 之實力

在定理 1 中，我們得到於包含4名選手之賽程表中，第 2 場賽程所模擬之假想選手 X 的實力 x。現在，我們進一步地將假想選手X 推廣，在包含 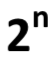名選手的賽程中，令選手 Q1 (我們用Q1取代A)晉升至第 n 節點時所遇上的假想選手為 Xn，如圖 6 所示，經過一番努力，啟樺推得下列定理3。


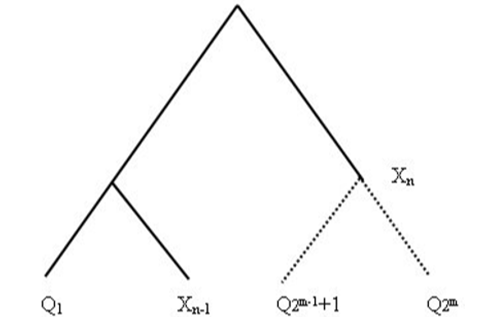
圖6. 選手 Q1晉升至第 n 節點時所遇上的假想選手為 Xn

定理 3 選手 Q1 於第 n 場賽程所遇上的假想選手 Xn之實力 xn為



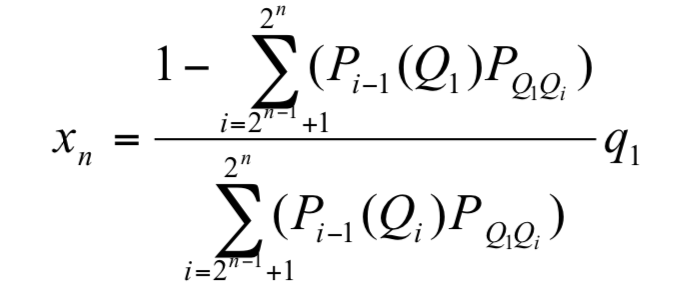
證明：
利用類定理 1 的方式，我們將第 n 場賽程所可能遇上的所有選手視為假想選手 Xn，由圖6 我們可以得到


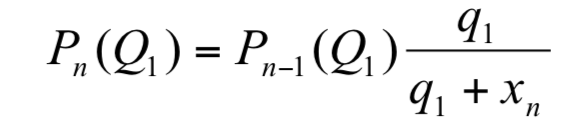
進一步推得


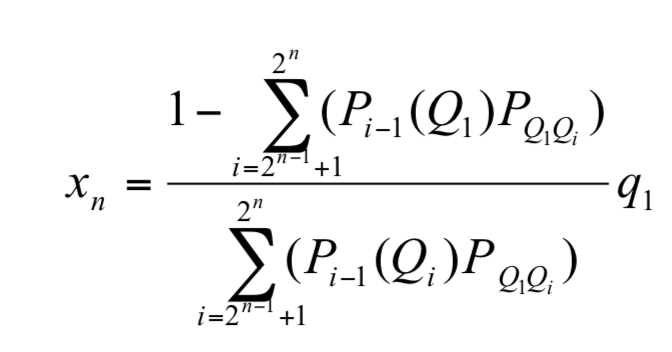
藉由假想選手 Xn，我們可以進一步判斷在未進行任何賽程之前，第 n 場賽程可能遇上的選手對Q1所造成的威脅。

經過一番努力，根據定理3，啟樺研究出包含8名選手的賽程中，如圖7，第 3 場賽程所可能遇上的對手也存在著威脅門檻，如下定理4，此定理的證明較為複雜，請讀者參閱文獻[1]。


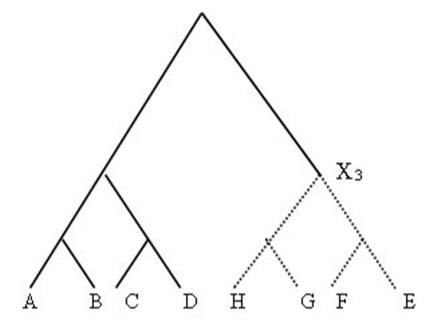
圖7. 包含8名選手的賽程

定理 4 若選手 A、F、G、H 的實力 a、f、g、h 滿足
則存在一威脅門檻 e0，若當 E 選手之實力 e > e0時，則 e 增加將使 P3(A)下降；當 E 選手之實力 e < e0，則 e 增加將使 P3(A)上升。

（二）包含 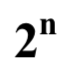名選手賽程之威脅門檻

在包含 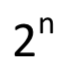人賽程中，由於假想選手 Xn 選手的實力 xn 展開過於龐大，無法對其微分。然而，啟樺仍能研究出當包含 人賽程之威脅門檻存在時，所須滿足的條件。如下定理5。
定理 5 若選手 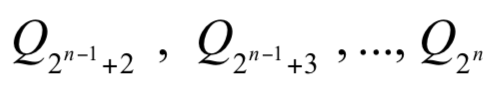的實力存在 ，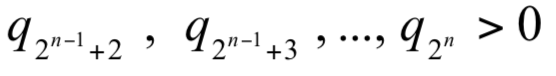
滿足 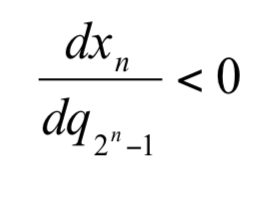則存在一威脅門檻 。

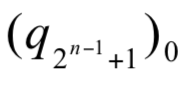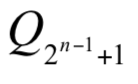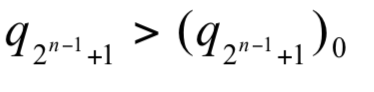當 選手之實力 時，則 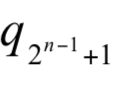增加將使 Pn(A)下降；

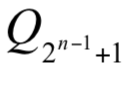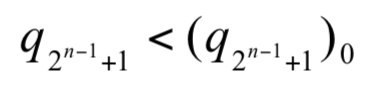當 選手之實力 時，則 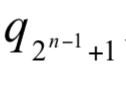增加將使 Pn(A)上升。

（三）勝率一般式

在賽程進行之前，選手們總想先秤秤自己的斤兩，算算自己於這場比賽中得到冠軍的機率。因此，如圖8，啟樺想要了解選手Q1晉升至第 n 節點的勝率一般式如何表示，經過一番努力推得定理6。


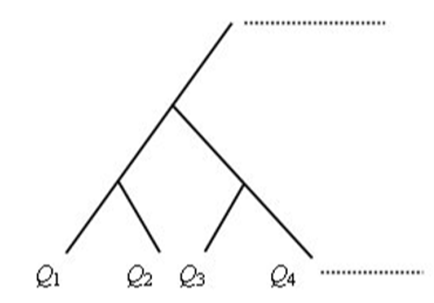
圖8 .Q1晉升至第 n 節點的勝率

定理6 選手 Q1 晉升至第 n 節點的機率為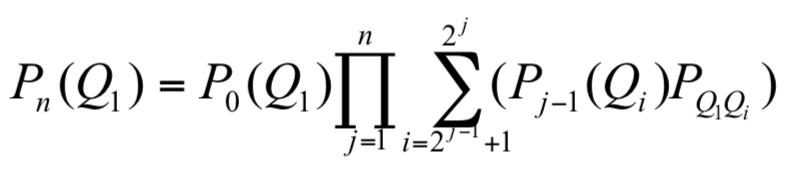

至此，啟樺對單淘汰賽程的研究已進入火熱的地步，隨著時間的推演，啟樺的研究更加深入與廣泛，內容創新有趣並且有更多的應用價值。在啟樺的研究報告中，共有16個定理和12個推論，本文僅介紹其中的一部分。接下來介紹的定理與推論，其證明請參閱文獻[1]。

由定理6與條件機率，我們可以進一步得到下列推論：
推論 2 選手 Q1 由第n節點晉升至第m節點的機率為

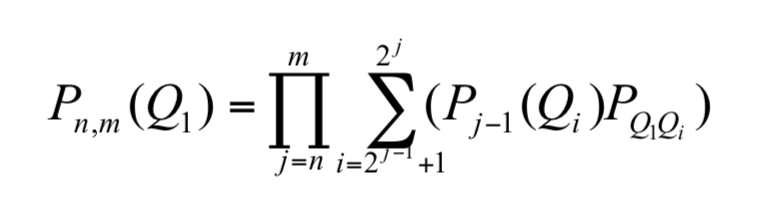
藉由假想敵人的概念，我們可以將賽程表簡化如圖9。則我們有：
定理 7 有一多項式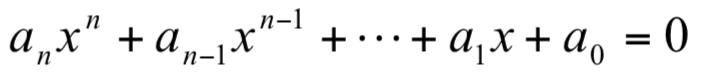 ，其 n 個根為 x1, x2, x3, ... ,xn，則選手 Q1 晉升至第 n 節點的機率為





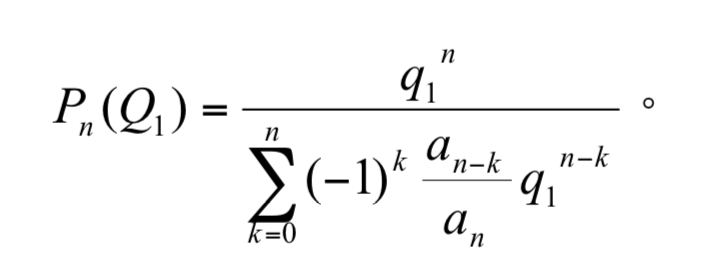
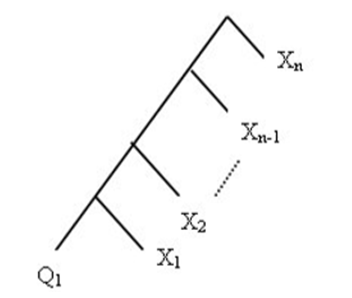
圖9. 推論2賽程

由定理7與條件機率，我們可以進一步得到：
推論 3 有一多項式 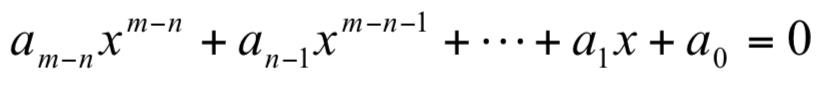，其m–n 個根為 xn+1, xn+2, ... , xm 則選手 Q1 由第 n 節點晉升至第 m 節點的機率為

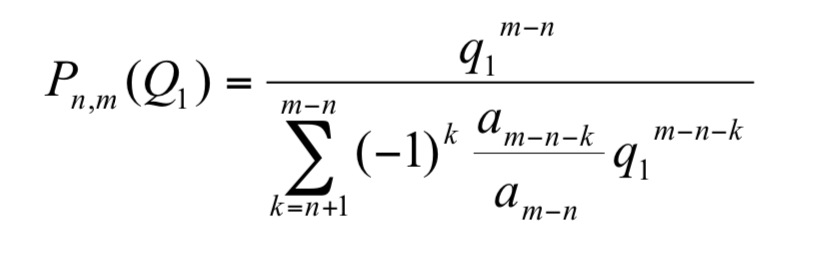
（四）自己實力上升對勝率的影響

直觀上，自己的實力增加，自己的勝率也會隨著增加。如圖1 包含 4 名選手的賽程表中，藉由檢驗自己的勝率是否為自己的實力之嚴格遞增函數，我們得到下列引理。

引理 1 於包含 4 名選手賽程表中，自己的實力增加使自己的勝率增加。

由引理 1 我們可得於包含 4 名選手的賽程表中，自己的實力上升使自己的勝率上升。那麼， 在包含 名選手之完全二元樹賽程中，我們證明亦是如此。

定理 8 於包含 2m 名選手之完全二元樹賽程表中，自己的實力增加使自己的勝率增加

（五）賽程安排對勝率的影響

接下來，啟樺想探討賽程的安排對勝率的影響，以及找出一張對選手自己最有利的賽程表，因此有了下列定義：

定義五：令 Fn(Qi,Aj)為選手Qi於賽程表Aj時晉升至第 n 節點的勝率實力比，即 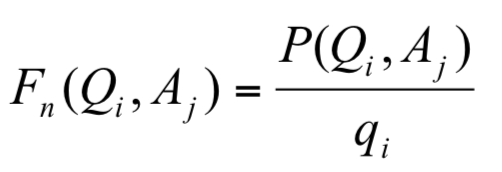，其中P(Qi,Aj)為選手Qi於賽程表Aj時晉升至第 n 節點的勝率。

我們常說:「實力增加，勝率就增加」，彷彿意味著實力與勝率有正比的關係。若以 Fn(Q1) 表示選手 Q1 晉升至第 n 節點的勝率實力比，則我們可以得到下列定理

定理 9 選手 Q1 晉升至第 n 節點的勝率實力比為

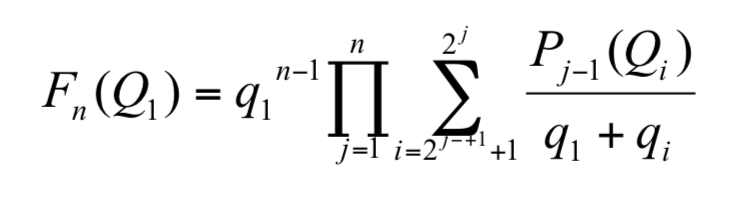
勝率實力比 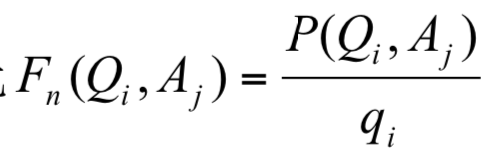愈高，代表賽程表Aj對Qi選手愈有利，藉此可推得對Qi選手最有利的賽程表。啟樺證明了下列定理：

定理 10 在包含 4 名選手的賽程中，對自己的最有利賽程表為與除自己以外之最弱選手於第一場賽程比賽。

此外，啟樺也歸納出包含 8 名選手的賽程中，對自己的最有利賽程表，詳情請參閱文獻[1]。

 結語

啟樺的研究報告內容，是非常豐富有趣的，因為篇幅有限，筆者僅節錄啟樺研究報告的一部分內容與讀者分享，對此專題研究有興趣的讀者，請閱讀文獻[1]，相信您一定會有豐富的收穫。

 參考文獻