壹、前言

筆者曾經在高中專題研究課程中提供了幾個開放性問題給學生們思考與探究，而其中有一個特別有趣的題目：

「將一個樂隊放在第一象限，若要從周圍外一層攝影整個隊伍，則需要幾個攝影點才能將所有人拍攝到？」

上述的問題源自於Laison &Schick(2007)，其中樂隊人員及拍攝者都站立在坐標平面的格子點上，所謂的格子點是指坐標都是整數的點。Laison &Schick(2007)已經有一些初步的成果如下：在不限制拍攝點的位置情況下，只需一個拍攝點，但這點離隊伍很遠。此外，Laison &Schick(2007)希望將拍攝點放在離隊伍較近的位置，而去尋找最少的拍攝點，這方面的研究，Laison &Schick(2007)還沒有提出明確的結果。

筆者的一位學生—盧崇文(2009)，特別鍾情於如上的題目，經過幾週的文獻探討，筆者和崇文擬定了初步的研究方向：

1.將拍攝點的位置限制在原點及x、y軸正向的格子點上，去尋找最少的拍攝點。例如下列圖1與圖2即為陣列2×2與陣列3×5的解決方法之一。

2.將拍攝點的位置限制在x軸的格子點上，其x坐標為0到m+1的整數，去尋找最少的拍攝點。

3.將拍攝點的位置限制在y軸上，其y坐標為非負整數，去尋找最少的拍攝點。

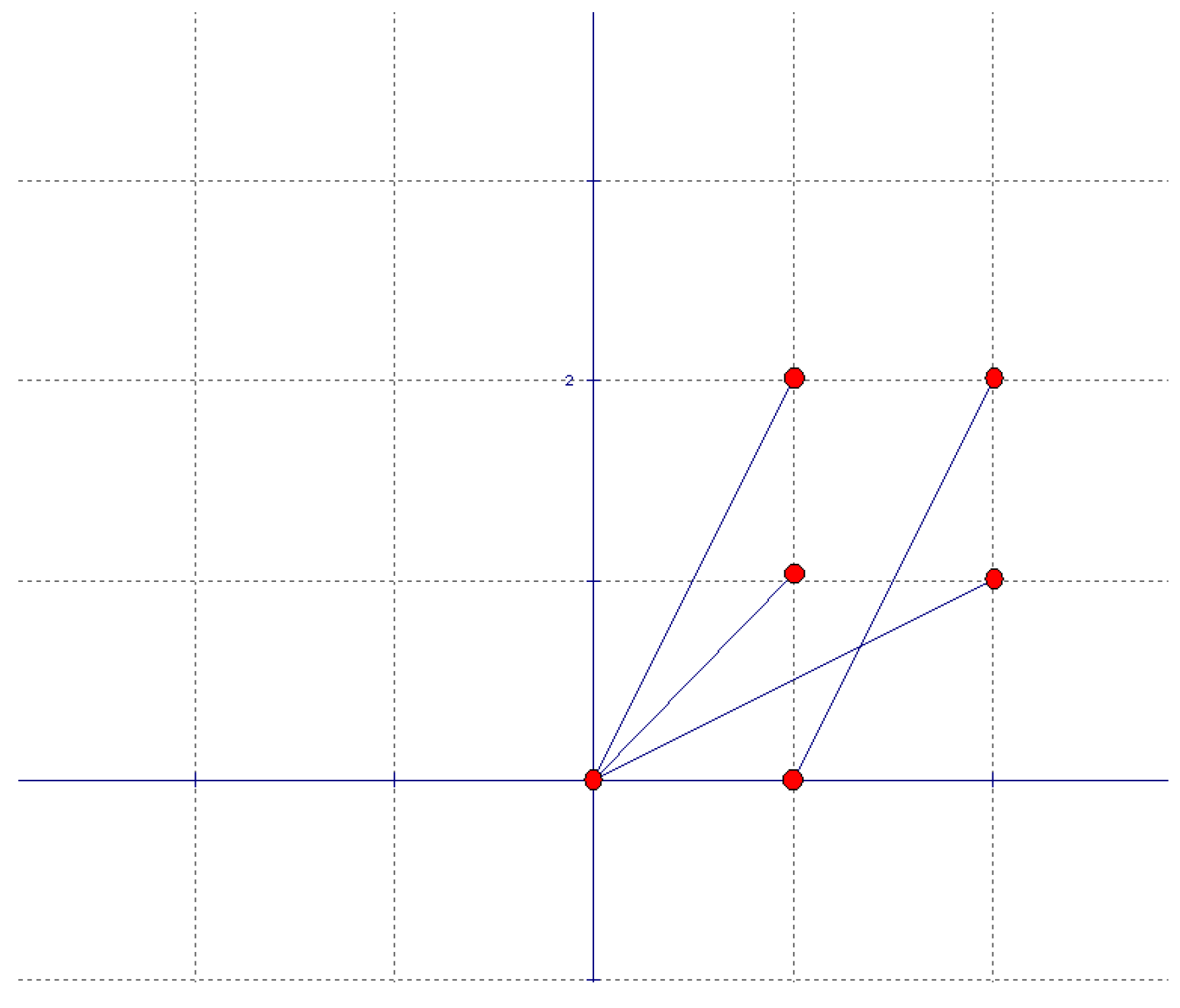圖1


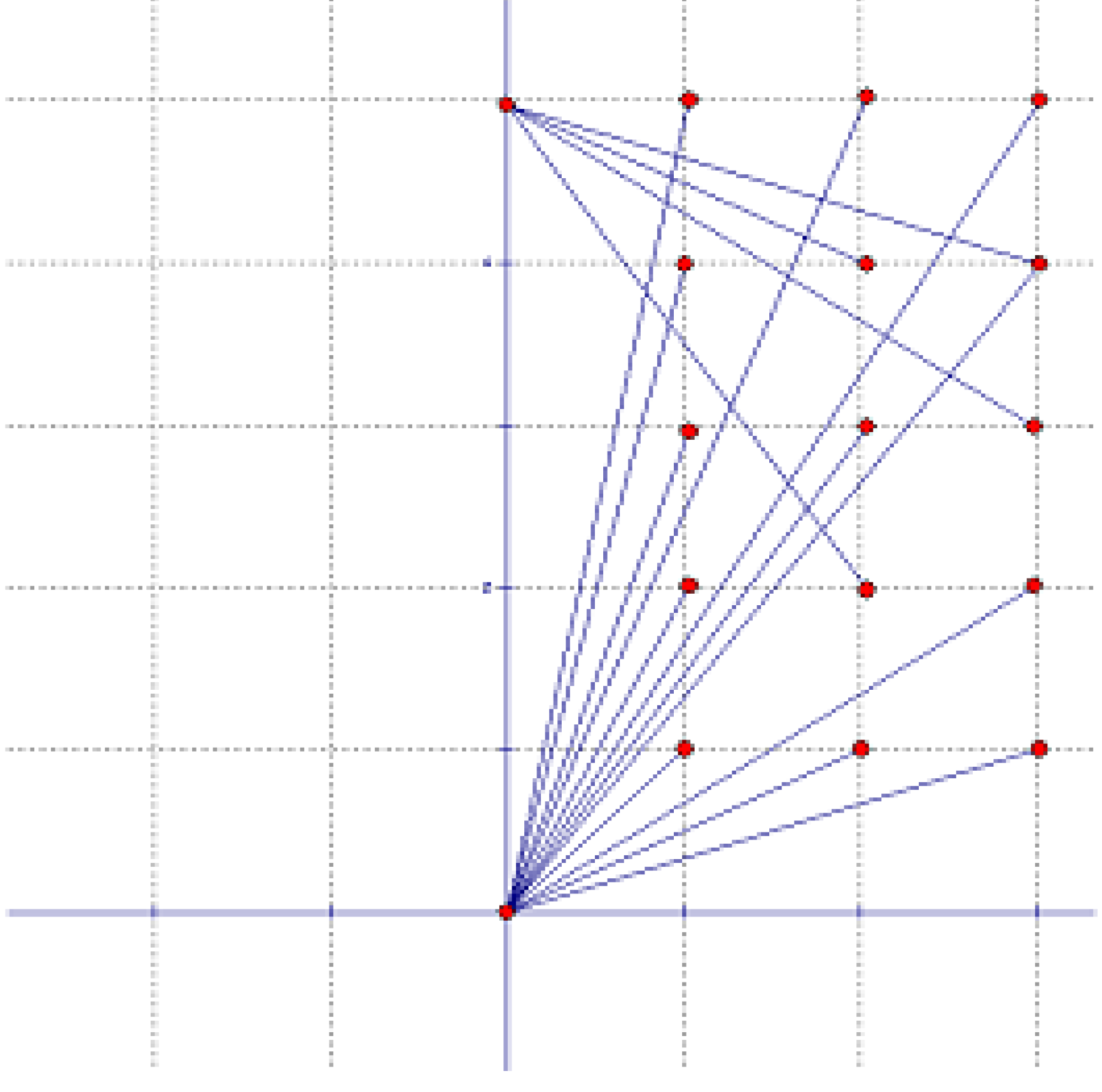圖2

就此，我們展開一連串驚喜有趣的探究過程，筆者將引述崇文的研究報告(盧崇文，2009)中最精華的部分與讀者分享。請讀者注意，本文中所提及的變數都是正整數或0。且本文介紹的圖表與定理皆取自盧崇文(2009)的研究報告與筆者的增減修正。

 貳、引導過程、研究方法與結果

在專題研究課程中，筆者通常會同時指導三、四組學生進行不同議題的探究，各組的進度會互有領先，哪一組提出的問題多，筆者與這組同學的互動時間就會比較多，這時期恰好是啟樺、崇文各一人一組，另外有兩組是兩人一組的團隊。

帶領專題研究需要耐心和細心，耐心是指研究過程中需要學生長時間的探究才能累積可觀有用的資訊量；這時期就像是農夫耕作時的鬆土期，將農地的土鬆開，尋找適合播種的土壤，然後播下種子，有耐心的澆水灌溉。

接下來，細心的觀察，看看幼苗何時冒出來？當幼苗成長時也要有策略地施肥，讓作物可以枝繁葉茂。印象中，啟樺的書桌上會有一本筆記本與正在研究中的文獻，筆記本中書寫著整整齊齊的計算式與評論；而崇文的書桌上總是放著一本計算紙，上面寫著詳詳細細的算式與數字，在專題研究課程中筆者會關心地詢問崇文：目前有何進展？崇文總是搔搔頭說：還在想。筆者總是叮嚀：從最簡單的例子開始研究。經過幾週的試探詢問，以及補充相關的文獻資料後，終於在某一次的課堂中，崇文站上了講台，在黑板上寫下一些數字，例如

(2,2r)，(3,3s)，(4,2t)，(6,2s)，(6,3t)。

一開始，筆者看不懂這些數字的涵義，但直覺告訴筆者，直得探究的幼苗冒出嫩芽了，所以筆者請崇文慢慢講述給筆者聽，這些數字代表的涵義。事實上，剛開始筆者無法理解崇文想要表達的內容，因為崇文講述的方式都是跳了好幾個步驟，筆者只好細心地捕捉一些關鍵資訊寫在黑板上，一一與崇文釐清，這才拼湊出一些具體樣貌如下。

一、在坐標平面上

我們將這個隊伍視為陣列m×n，安置在坐標平面上觀察。以第一象限的 (1,1)為起點，隊伍依序在格子點上排列，希望拍攝點的位置是在陣列的外一層，因為對稱關係，我們將拍攝者的位置限制在原點及x、y軸正向的格子點上，且x坐標不超過m+1。令第1個拍攝者的位置為，第2個拍攝者的位置為，…，第n個拍攝者的位置為。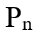

現在，假設這是1個 m×n的隊伍，m, n為正整數，我們從原點去拍攝這個陣列，其中x, y坐標互質的點，可以從原點看見。而有些點會被其他點擋住，例如:(2,4) (3,6)等等。觀察這些被擋到的點，都有共同的現象：“x, y坐標不互質”。經過思考，得到一個結論。

定理1 x, y坐標不互質的點，從原點看，會被擋住。

定理1的證明: 設C(mx,my) ( m為自然數 且>1 )為x,y坐標不互質的點

令A(0,0),B(x,y)，則直線AB的斜率為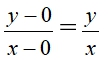，直線BC的斜率為。

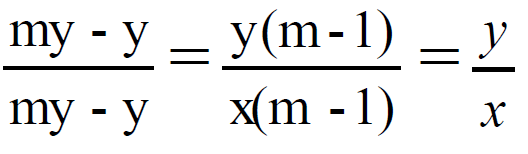所以直線AB的斜率等於直線BC的斜率，故兩直線重疊或平行。點B在直線AB之上，也在直線BC之上，所以A、B、C三點共線。故A點就無法觀察到C點。

相對於定理1，設P點坐標為(x,y)，若x,y互質，則由原點O可拍攝到P點。

觀察這些被擋住的點，經由因數與倍數的關係，不難發現：在x = 2 這條直線上，被擋住的點為 (2,2)，(2,4)，(2,6)，…，(2,2n)；在x=3這條直線上，被擋住的點則是(3,3)，(3,6)，(3,9)，…，(3,3n)；而在x=6這條線上，則是(6,2)，(6,4)，(6,6)，…，(6,2n)及(6,3)，(6,6)，(6,9)，…，(6,3n)。因此，引用定理1即可得證兩個結論如引理1與引理2。

引理1 在x=a這條直線上，原點拍攝者拍不到的點，其y坐標會是a的質因數的倍數，即y坐標與a不互質的點。

若從(1,0)這個點去拍攝這個陣列m×n，在直線x =3上觀察不到的點為(3,2n)。在直線x = 3上，從原點觀察不到的點為(3,3n)。所以若由(1,0)，(0,0)這兩個拍攝點同時拍攝不到的點為(3,6n)。

引理2 對拍攝點(k,0)而言，直線x=m上看不到的點，其y坐標是m-k的因數的整數倍。
引理2的證明：對於所有的點、、…、其中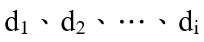為m-k的因數，a為任意正整數。若以(k,0)為新原點，則平移變換為。而m-k與adi兩數不互質，故由定理1得知拍攝點(k,0)拍不到點。

上述的定理1及兩個引理彷彿是本專題研究的一絲曙光。了解到此研究與整數中的因數倍數關係具有關聯性，雖然說有了這層體悟，但是問題的複雜度仍然讓崇文陷入迷霧中許久。累積了幾週的努力耕耘，崇文突然想起了在高一上學期，筆者曾經講授過基本的數論性質，其中有一個與輾轉相除法原理相關的定理可以引用，如下定理2。

定理2 若N和R互質，則N與PN–R互質。
証明: 因為PN–R=NP–R由輾轉相除法原理得知PN–R和N的最大公因數等於N和–R的最大公因數，故得證。

接下來，我們來看看如何利用定理1、2與引理1、2來探討本研究。一開始，筆者策略性的引導，筆者建議崇文依據觀測點的位置做分類討論。因此，我們將觀測位置大致分成三類。

（一）將拍攝者的位置限制在原點及x、y軸正向的格子點上

首先筆者建議崇文先固定m值，而n值是任意正整數，由最簡單的m=1開始，即從陣列1×n開始探討，再將m值逐步增加，看看是否有規律可循，討論的方法如下。

假設m為固定正整數，n為任意正整數，若限制拍攝者的位置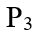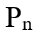，，，…，，為x軸正向與y軸正向上的點，且其x坐標不超過m+1。將陣列m×n放置第一象限討論，以第一象限的(1,1)為起點，隊伍依序在格子點上排列，可得到以下一系列的推論。証明中所使用的文字符號m,n,r,s,t,u…等都是正整數。雖然推論頗多，但是為了本文的連貫性，筆者仍將其一一羅列如下。

推論1 陣列1×n需1個拍攝點(0,0)能全部入鏡。
證明：1與n互質，所以由點(0,0)拍攝能全部入鏡。

推論2 陣列2×n需2個拍攝點(0,0)與(3,0)能全部入鏡。
證明：
可將x=1上的點全入鏡，則可以可將x=2上的點全部入鏡，整個隊伍皆為所見。

上述兩推論較為簡單，接下來的推論需要用到坐標平移變換的概念，將新增的拍攝點視為新原點，則原來拍攝不到的點可由前述的定理與引理來協助證明可被新增的拍攝點拍攝到，如此陣列中的所有點皆可被拍攝到。注意其中的符號"→"代表平移變換。

推論3 陣列3×n需2個拍攝點(0,0) 與 (0,5) 能全部入鏡。
證明：
所不能看見的點為(2,2r)、(3,3s)，r，s為正整數，但對視線而言，將(0,5)視為新原點，點(2,2r)變換成(2,2r-5)，因為由定理2得2與2r-5互質，點(2,2r)可由拍攝到，故在直線x=2上的點可全入鏡。至於在直線x=3上的點，(3,3s)→(3,3s-5)，由定理2得3和3s-5互質，點(3,3s)也可由拍攝到。故陣列3×n可由2個拍攝點(0,0)與(0,5)能全部入鏡。

推論4 陣列4×n需2個拍攝點(0,0)與(0,5)能全部入鏡。
證明：
所不能看見的點有(2,2r)，(3,3s)，(4,2t)，由觀察，將視為新原點後，(2,2r)→(2,2r-5)，(3,3s)→(3,3s-5)，(4,2t)→(4,2t-5)，平移變換後，這些點的x與y坐標都互質，故皆可以入鏡。

推論5 陣列5×n需2個拍攝點(0,0)與(0,7)能全部入鏡。
證明：
所不能看見的點有(2,2r)、(3,3s)、(4,2t)、(5,5u)。經觀察，將原點平移至後，即將視為新原點後，
(2,2r)→(2,2r-7)，(3,3s)→(3,3s-7)，(4,2t)→(4,2t-7)，(5,5u)→(5,5u-7)。
平移變換後，這些點的x與y坐標都互質，故皆可以入鏡。

推論6 陣列6×n需3個拍攝點(0,0)、(7,0)與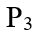(0,7)能全部入鏡。
證明：
，所不能看見的點有(2,10r)，(3,6s)，(4,6t)，(5,10u)。將原點平移至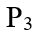後
(2,10r)→(2,10r-7)，(3,6s)→(3,6s-7)，(4,6t) →(4,6t-7)，(5,10u) →(5,10u-7)。
平移變換後，這些點的x與y坐標都互質，故可以全入鏡。

推論7 陣列7×n需3個拍攝點(0,0)、(7,0)與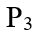(0,11)能全部入鏡。
證明：
藉由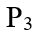，，可以將陣列6×n 的範圍看完，故只多出x=7這排。和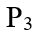可將x=7這直線上的點看盡，故可全入鏡。

推論8 陣列8×n需3個拍攝點(0,0)、(7,0)、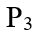(0,11)能全部入鏡。
證明：
跟7×n類似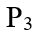，、 、可以將陣列7×n的範圍看盡，其餘在直線x=8上的點，又可以由、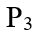看盡，故可以全入鏡。

推論9 陣列9×n需3個拍攝點(0,0)、(7,0)、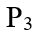(0,11)能全部入鏡。
證明：
跟8×n類似、、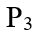可以將陣列8×n的範圍看盡，其餘在直線x=9上的點又可以由、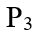看盡，故可以全入鏡。

上述的推論一度讓我們樂觀地認為，陣列m×n的拍攝點數目似乎可以使用數學歸納法去推得結論。但事實上並沒有那麼簡單，當m=10時，找拍攝點需要較複雜的方法。

推論10 陣列10×n需4個拍攝點(0,0)、(5,0)、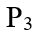(0,11)與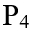(8,0) 能全部入鏡。
證明：
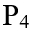在直線x=10上，拍攝不到的點 為(10,2r)、(10,5s)，的死角拍攝不到的點(10,5t)，拍攝不到的點為(10,2u)。、 、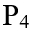共同拍攝不到的點為(10,10v)，
再以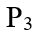為新原點觀察後，(10,10v)→(10,10v-11)，此x、y坐標互質，故可以全入鏡。
所以若要使x=10這線上的點皆被看盡，可以利用這個原則。(0,0)是固定的，所以要調整以及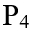讓最後被擋到的點為(10,10v)，再使用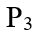(0,r)其中r為大於10的某一個質數，去觀察(10,10v)，以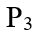(0,r)為新原點，則點(10,10v)→(10,10v-r)由定理2得知10和10v-r互質，故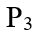(0,r)可以拍到點(10,10v)，因此由、、、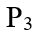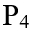四點就可以將x=10這排看盡。
所以(5,0)與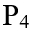(8,0) 可達成目的，再將此4點從新審視直線x=1至x=9恰好可以全部入鏡。

在m≧11以後，找拍攝點需要更複雜的演算方法。現在以陣列20×n為例，來說明使用的演算方法。
先將小於或等於20的所有擁有2個以上質因數的數列出來:6,10,12,14,15,18,20，接著拍攝點最佳的位置如下所示，其中k為非負整數。



只要拍攝點符合上述的所有條件，再加上y軸上取一拍攝點(0,r),r為適當的質數，一般會取r為大於m的最小質數，這個陣列就能全部被拍攝到。
原因說明如下：
以直線x=6上的點為例，若拍攝點為原點(0,0)與A、B兩點，一起拍攝直線x=6上的點，由引理1得知原點(0,0)拍攝不到的點為(a,b)，其中a與b不互質，由引理2得知拍攝不到的點為(6,2n)，拍攝不到的點為(6,3n)，因此這三個拍攝點會讓x=6直線上拍不到的點剩下點(6,6t)，再把這個點交給拍攝點(0,r)，以(0,r)為新原點使得(6,6t)→(6,6t-r)，若r為大於6的質數，則6和r互質，再引用定理2可得6和6t-r互質，所以點(6,6t)可以由點(0,r)拍攝到。
同理，在直線x=10上的點可由原點(0,0),,與y軸上的點(0,r),等四個點，即可全部拍攝到。其中r為大於10的質數，例如取r=11即可。
在直線x=12上的點可由原點(0,0),與y軸上的點(0,r),等四個點，即可全部拍攝到。其中r為大於12的質數，例如取r=13即可。
在直線x=14上的點可由原點(0,0),與y軸上的點(0,r),等四個點，即可全部拍攝到。其中r為大於14的質數，例如取r=17即可。
在直線x=15上的點可由原點(0,0),與y軸上的點(0,r),等四個點，即可全部拍攝到。其中r為大於15的質數，例如取r=17即可。
在直線x=18上的點可由原點(0,0),與y軸上的點(0,r),等四個點，即可全部拍攝到。其中r為大於18的質數，例如取r=19即可。
在直線x=20上的點可由原點(0,0),與y軸上的點(0,r),等四個點，即可全部拍攝到。其中r為大於20的質數，例如取r=23即可。
所以若要滿足上述各種情況，y軸上的拍攝點取點(0,23)即可。
而x軸上的拍攝點取能涵蓋ABCDEFGHIJKLMN的點即可，且要找出拍攝點數目的最小值，其演算方法如下步驟。

1.先以其x坐標變化量最大者(即其a±dk中d值最大者)為基準做為拍攝點，上列中以變化量最大。可能的拍攝點有(15,0) (13,0) (21,0) (7,0)。先考慮(15,0)，BDFGHLN取適當的k值也都可成為(15,0)。

2.剩餘的變化量最大的為，可能的拍攝點有(16,0)(14,0)(20,0)(10,0)，先以(16,0)測試，成功的有EIJKM。剩下的AC則用(8,0)就可符合。

3.再回到步驟2使用(14,0)測試，直到(16,0) (14,0) (20,0) (10,0)這4個點都測試完後，再回到步驟1測試(13,0) (21,0) (7,0)。

4.最後再找出最少點的路線。

上述演算方法可由下列圖3的樹狀圖表示

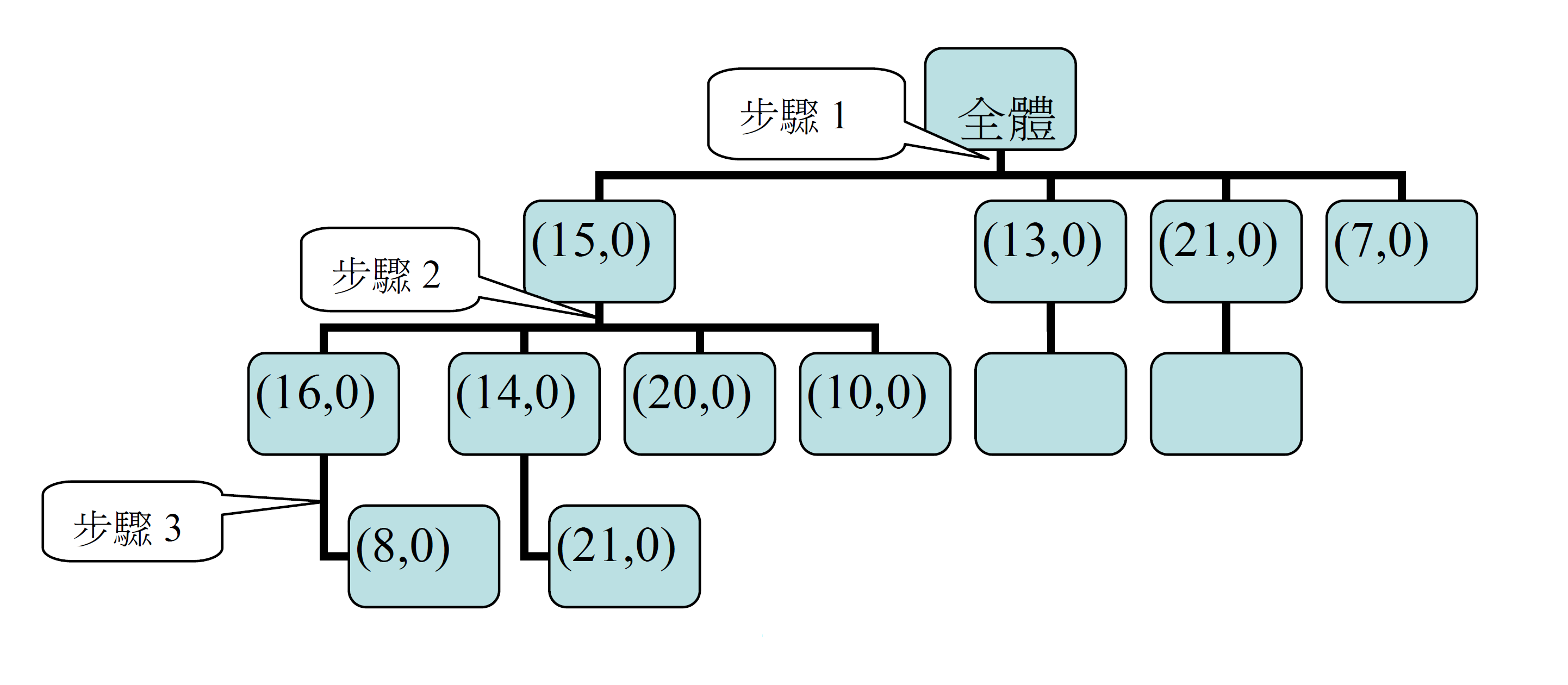
圖3

由上述演算方法可得下列推論。

推論11 陣列20×n需5個拍攝點(0,0)、(15,0)、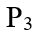(8,0)、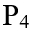(16,0)、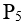(0,23)。
證明：
想讓x=6、10、12、14、15、18、20這7排都符合要求，所以拍攝點的x坐標必須滿足，找一找之後，發現(15,0)、(16,0)、(8,0)可以完成。
所以，使用(0,0)、(15,0)、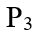(8,0)、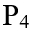(16,0)、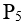(0,23)可以把陣列20×n全部拍攝到。

若讀者未能理解上述的演算方法，請讀者參閱崇文的研究報告(盧崇文，2009)，內容中有m=11到m=25的詳細推論。
接下來，我們介紹由上述的演算法與推論綜合整理而成的定理3。此定理在崇文的報告中沒有詳細證明，筆者補上證明如下。定理3也可以說是我們設定的第一個研究方向的重要結論。

定理3 設m是大於5的固定正整數，在陣列m×n中，拍攝者的位置限制在原點及x、y軸正向的格子點上，且x坐標不超過m+1，則需要個拍攝點就可以拍攝整個陣列。
證明：
設不大於m的正整數中含有二個以上質因數的合成數有等，共h(m)個，ci為其中任一個，而其質因數有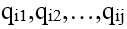等，j為某固定正整數。若一點集合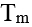，其元素是x軸正向上的點且它們的x坐標涵蓋所有的型態，其中k為非負整數，且元素個數為最少者，則我們定義的元素個數。
所以，使用點集合Tm中的點再加上(0,0)與P(0,r)兩點，其中r為大於m的最小質數，就可以把陣列m×n全部拍攝到。故需要個拍攝點就可以拍攝整個陣列。

（二）將拍攝者的位置限制在原點及x軸正向的格子點上

假設m為固定正整數，n為任意正整數，若拍攝者的位置，限制在x軸上且其x坐標為0到m+1的整數，則對於m×n陣列則有下列結果。証明中所使用的符號m,n,r,s,t,…等都是正整數。
因為不能在y軸正向上布置拍攝點，所以定理3所使用的方法就無法執行，因此必須多一些拍攝點布置在x軸的正向上，經過筆者和崇文的討論，有下列的結果。

定理4 在陣列m×n中，拍攝者的位置限制在x軸上且其x坐標為0到m+1的整數，若m=4k則恰需要m/2個拍攝點；若m≠4k則恰需要[m/2]+1個拍攝點就可以拍攝整個陣列，其中[x]表高斯函數。
證明：若要將x=t直線上的格子點完全拍攝到，則必須在(t-1,0)或(t+1,0)設置一個拍攝點，因為如果其他位置的拍攝點為，當s與所有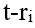皆不互質時，坐標為(t,s)的點將會看不到，而且一個拍攝點最多只能完全拍攝兩直線。因此將正整數m分成4k,4k+1,4k+2,4k+3四類。每4行一組，把拍攝點放置在中間兩行的x軸上(如圖4)是最佳的方法，則m=4k時，恰需要2k個拍攝點。m=4k+1時，恰需要2k+1個拍攝點就可以拍攝到整個陣列，而m=4k+2與m=4k+3，則恰需要2k+2個拍攝點就可以把整個陣列拍攝到。故得證。


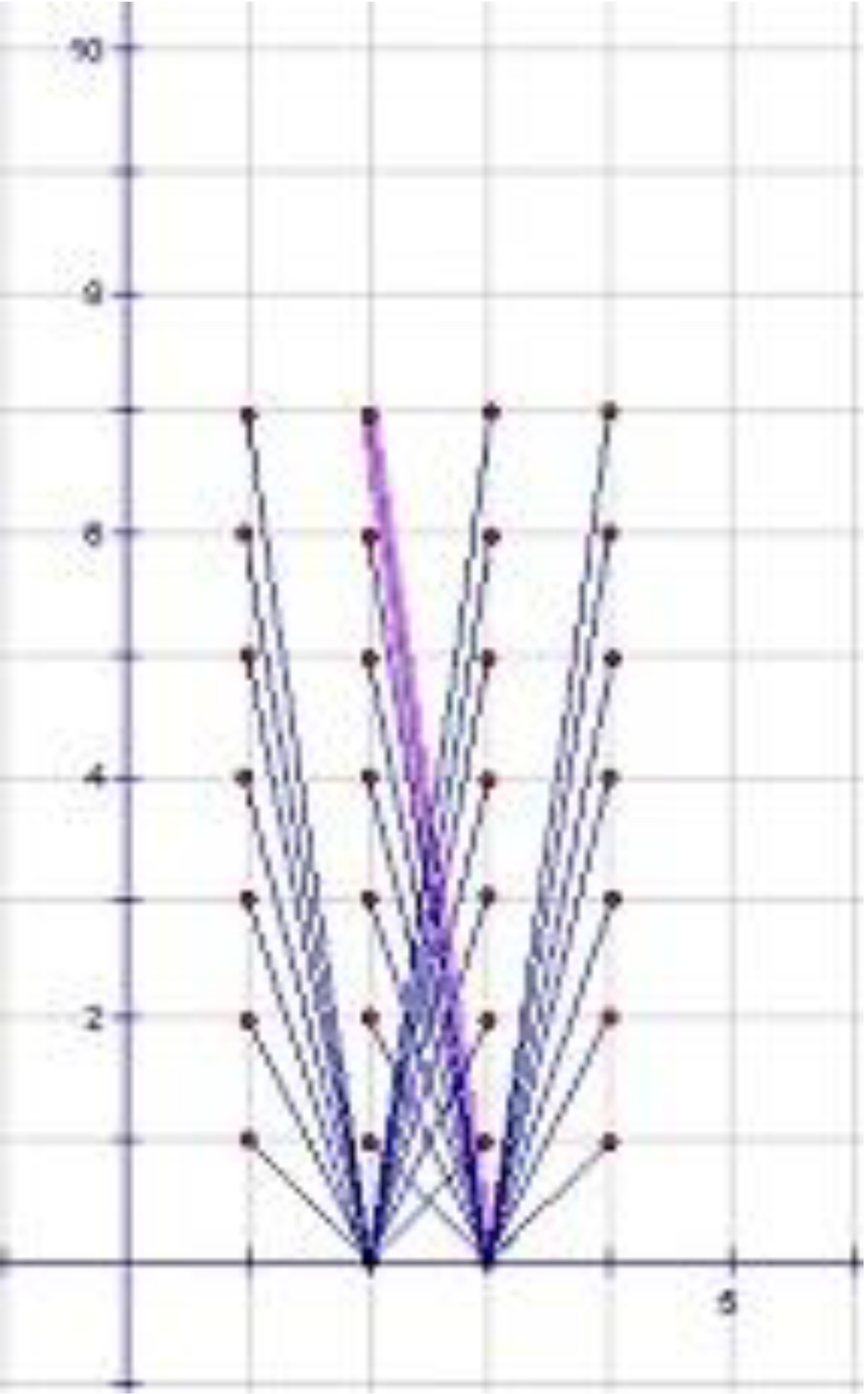
圖4

（三）將拍攝者的位置限制在原點及y軸正向的格子點上

有了定理3的經驗，若拍攝者的位置限制在原點及y軸正向的格子點上時，筆者建議崇文由y坐標是質數的拍攝點開始探討，經過崇文的研究，發現了解決的方法，下列內容以10×n陣列為例說明。
先將小於或等於10的所有擁有2個以上質因數的數列出來：6、10。接著將這些數字因數分解找出他們的質因數，而拍攝點的y坐標就是6與10的質因數，即為2、3、5，接下來再增加原點以及(0,r)，r為大於10的質數，例如可取r=11，即可將這個陣列完全拍攝到。
原因：以原點和(0,r)就可以把x坐標只含1個質因數的直線上的格子點完全拍攝，也就是除了x=6和x=10這兩行之外的直線，都能由原點與(0,r)完全拍攝。而藉由(0,2)、(0,3)還有原點能使的x=6這直線上拍攝不到的點剩下(6,6k)，k是正整數，(0,2)、(0,5)還有原點則能使x=10這直線上拍攝不到的點剩下(10,10s)，s是正整數，這兩種型態的點最後都能由(0,r)拍攝，所以10×n這個陣列，可以被(0,2)、(0,3)、(0,5)、(0,0)、(0,r)，所拍攝，其中r為大於10的質數，可取r=11。藉由這個例子，將其推廣為下列結論。

定理5 設m是大於5的整數，n是任意正整數，在陣列m×n中，若拍攝者的位置限制在y軸上且其y坐標為非負整數，則需個拍攝點，就可以拍攝整個陣列，其中函數代表不大於m的所有含2個質因數以上的合成數的質因數個數，重複的質因數只算一次。
證明：將不大於m的所有擁有2個質因數以上的合成數列出來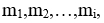：再將其因數分解找出他們的相異質因數共個，而拍攝點的y坐標就是這些質因數，接下來再增加原點(0,0)以及(0,r)，r為大於m的最小質數，即可將這個陣列完全拍攝到。故共需個拍攝點。

當崇文提出上述想法時，筆者直覺的聯想到與計算質數個數有關的函數，因此筆者建議崇文研究質數計數函數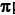(x)，這是一個用來表示小於或等於某個實數x的質數的個數的函數。經過一番的討論，令人感覺到特別驚喜的是，我們發現函數κ(m)與計算質數個數的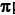函數竟有如此巧妙的關係，如定理6所示。

定理6 函數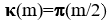，其中函數中代表不大於m/2的所有質數個數。
證明：對任意質數p而言，其所形成的合成數中，最小者為2p，若2p≦m，則p≦m/2，故得證。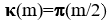

二、在坐標空間中

在坐標平面上的陣列拍攝研究有了些許成果之後，筆者建議崇文將研究結果推廣到空間坐標中。現在我們想將平面上的樂隊陣列拍攝問題推廣至空間中的恆星陣列拍攝問題，這需要空間中的直線方程式的概念，因此筆者建議崇文先熟悉高二下學期的數學課本中的空間坐標系相關內容。
接下來，我們定義坐標空間中由恆星組成的陣列r×s×t：
以第一卦限的(1,1,1)為起點，恆星依序在第一卦限的格子點上排列，形成陣列r×s×t。若假設宇宙中的恆星為位於第一卦限的陣列r×s×t的格子點上，而我們從原點去觀察這些星星，會發現有些恆星看不到。去探索這些恆星的位置，可以使用平面上類似的方法，對於恆星(x,y,z)，若x,y,z不互質，這個恆星就會被擋住。

定理7設P點坐標為(x,y,z)，若x,y,z不互質，則由原點拍攝不到P點。
證明：
設某恆星A所在的座標為 (ma,mb,mc)，(a,b,c)=1，那麼從原點去觀測恆星A，因向量 =(ma,mb,mc)，所以直線OA的方向向量可以表示為(a,b,c)。若又存在某恆星B(a,b,c)，因向量 =(a,b,c)，直線OB的方向向量也為(a,b,c)，所以A和B以及原點O在同一條直線上，故若從原點觀察A會被B點擋住。

相對於定理7，設P點坐標為(x,y,z)，若x,y,z互質，即最大公因數為1，則由原點可拍攝到P點。


接下來，崇文研究了許多空間中的觀測情形，因為內容較為複雜，所以不在此贅述，對此主題有興趣的讀者請參閱文獻(盧崇文，2009)。事實上，運用定理7，我們可以將坐標平面上的結果推廣至坐標空間中，如下定理8所述。

定理8 如果拍攝者的條件限制在原點O與x軸和y軸上的正向上，則即使到3維空間，仍然可使用平面上的拍設點拍攝。
證明: 已知若在平面上，可以被拍攝到的點，最終的x,y坐標互質，那麼即使到了3維空間，只要該點的x,y坐標互質，無論其z坐標為何，該點的x,y,z三個坐標必互質，故該點即被觀測到。
如果將觀測陣列問題推廣至n維空間，則我們也可推得如下的定理9。

定理9 如果拍攝者的條件限制在原點O與x軸和y軸上的正向上，則即使將陣列推廣到N維空間，仍然可使用平面上的拍設點拍攝。
證明: 已知若在平面上，可以被拍攝到的點，最終的x,y坐標互質，那麼即使到了N維空間，只要該點的x,y坐標互質，無論其他軸向的坐標為何，該點的所有坐標必互質，故該點即被觀測到。
行文至此，或許讀者會認為此研究到此似乎已完整結束，但事實並非如此。筆者試著將可以繼續深入探究的方向與猜想列舉如下，提供有心探究此主題的學生們一些參考的方向。

（一）猜想：

（二）探討平面上特殊形狀之陣列，所需最少拍攝點的問題　

（三）在空間中，以最佳的演算法找尋拍攝點的方法，尚待討論

事實上，筆者也曾經進一步指導學生做後續的研究，並且獲得了更豐富的成果，或許將來有機會可以再次與讀者們分享。