壹、前言

西元2016年東吳大學以英語授課的「數學建模概論」課程，來了一個德國旁聽生，當老師講到曲線與不等式在處理1962年古巴飛彈危機的應用時，德國學生說：「我們念高中時，已經被要求對整個故事有完整的了解，知道這些曲線與不等式的應用」。台灣的高中生學了曲線及不等式之後卻還在問「學數學有什麼用」？

西元2005年中央社有一則新聞報導：「在一九九五、九六台海飛彈危機、九二一大地震、世界貿易組織（WTO）入會談判、嚴重急性呼吸道症候群（SARS）疫情等台灣近十年重大歷史事件中，一群曾經實際參與危機處理或擔任幕僚作業的各界人士，在處理危機的過程曾遭遇系統工程設計、理論與實務的連結問題、實際操作與管控等諸多問題。他們透過跨領域朋友的合作，開發出許多解決問題的工具，諸如賽局與謀略作為、問題本質分析、指管通資情監偵（C4ISR）系統工程原理、衝突與談判、情報研判、兵棋推演（War game）、願景與戰略規劃、危機管理程序等。這些工具彌補了理論與實務中間的鴻溝，並經由工作中的實踐、返饋，逐漸成為解決問題的操作準則，或標準程序。」(中央社，2005)。上述過程中「數學建模」是操作實務與建構理論的關鍵橋樑。

 貳、數學建模的定義

絕大多數國內外的數學教育研究者談到「數學建模」時，大都按照(Blum, Galbraith, & Niss, 2007； Borromeo Ferri 2006；Kaiser, et al. 2006) 的觀點，考慮數學建模循環過程 (modelling cycle) 之「數學外部世界」 (extra-mathematical world) 與「數學世界」 (the mathematical world) 互相影響的情形，以Blum and Leiβ(2007) 所畫的「The modelling cycle」六個面向圖來表示數學建模的六個步驟。

1.理解(Understanding)「真實情境」(Real situation)；

2.簡化/建構(Simplifying/Structuring) 「真實模型」(Real model)；

3.將「真實模型」數學化(Mathematizing)成「數學型模」 (Mathematical model)；

4.進行數學、推理運算…等數學工作(Working mathematically)求「數學解」(Mathematical results)；

5.將「數學解」解釋(Interpreting)成「真實解」(Real results)；

6.驗證(Validating)由「數學解」轉成「真實解」是否能解決真實世界的問題。

我們將The modelling cycle（Blum and Leiβ, 2007)的圖形，以中文表示如下：


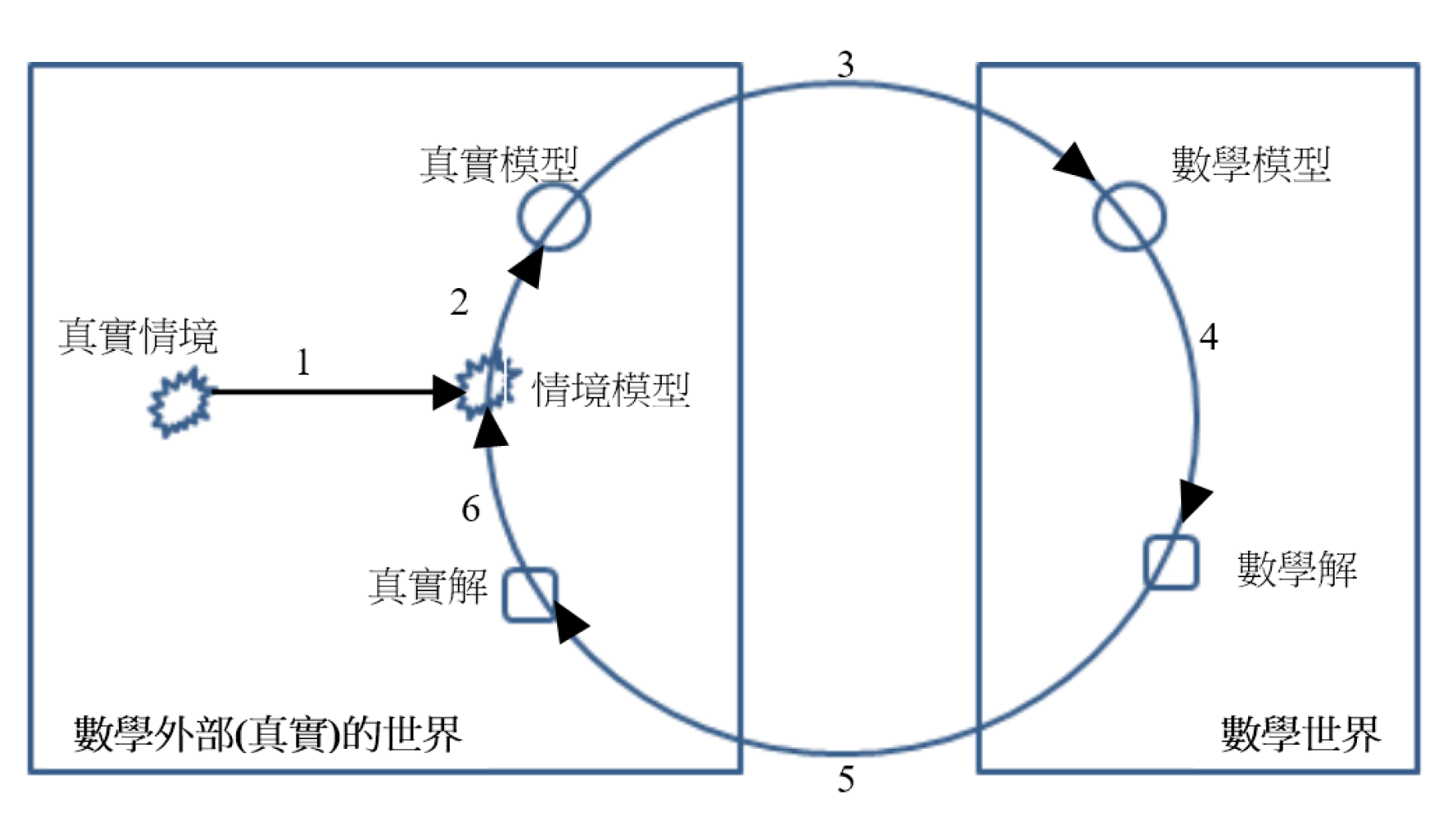圖一.The modeling cycle(資料來源:Blum and Leiß, 2006)

我們認為以[圖一]所表示的數學建模之定義與數學建模的步驟，是有缺失，可能造成數學建模與實務之間產生誤差的！我們以下面兩節來說明造成學校的「數學建模教育」與「國家社會所需的數學建模」有鴻溝之原因。

 參、「生活的數學」抑或是「數學的生活」

西元1960~1970年代的台灣，不少台灣的學生有家庭代工之生活體驗；放學後，在家裡繡一件較複雜的手工針織毛衣，工資就能買一碗陽春麵。一般家裡，可能大姐擅長十字繡，小妹擅長平針繡，一件衣服需要兩種繡法時，不必經由[圖一]右邊的「數學世界」，兩姐妹就知道如何分工合作來最大化生產速度。甚至，合作繡花的兩人如果不是姐妹，而是鄰居，同樣不必經由數學建模六步驟，就能以合作繡花的「邊際貢獻度」來分錢，筆者有這樣的真實生活經驗。這是在生活中「不自覺」地使用數學建模的例子，可以說是「生活的數學」，這對姐妹不需要「數學的生活」—先學好數學再應用到生活上。以下給一個更極端的例子！

西元2014年的縣市長選舉，為了理解對手是否可能以其龐大的財力，利用「地下簽賭」影響選情，某候選人的智囊拜訪了「營業額」很巨大的「地下簽注站」。簽注站的「負責人」(俗稱「組頭」)沒學過「數學」更遑論「機率與統計」，但是組頭憑他的「生活經驗」，頭頭是道地解釋了他們如何操作一個，甲與乙兩位候選人，不管誰勝誰負，莊家也就是組頭，都不會受影響，淨賺「手續費」(俗稱「抽頭」)」的「機制」或者稱「模型」。組頭解釋他的「真實解」：接受簽注時，一定要「喬」到，可以從賭輸的一方所沒收的賭金，足夠支付賭贏的一方的彩金，淨賺「手續費」，如果候選人雙方民調差距很大，賭客一面倒地押注某候選人，可用調整「賠率」或「讓票」的方式，來影響賭客的投注意願，讓投注兩位候選人的金額很接近，如果押注雙方的賭金差距太大，組頭無法負荷，就把多出來的賭金轉給其他營業額更大的組頭，而營業額更大的組頭，是合併了其他縣市選舉甚至與國際賭場合作，把選舉、運動、賽馬…等合併計算，原則就是要「喬」到，不管賭客誰輸誰贏，從賭輸的一方所沒收的賭金，可以支付賭贏的一方彩金。

用數學語言來說，就是組頭讓自己與所有的賭客對賭之勝負彩金的期望值等於零，純賺「手續費」，組頭是憑生活的經驗，不自覺地使用機率期望值，即「生活的數學」，並不是先學機率統計再應用到生活上—「數學的生活」。當然，我們也可以說，西元2004年的總統大選的319槍擊案，造成許多沒經驗的組頭輸到破產落跑，是因為他不懂機率統計，不懂得把數學應用到生活上—過「數學的生活」。

從以上兩個例子，我們可以看出[圖一]中的真實世界裡「情境模型」、「真實模型」與「真實解」在真實世界是可以雙向溝通的，亦即，有些真實問題不必透過數學的世界就能找到解「真實解」。 我們認為[圖一]有不少的缺點，建議改成下圖，會使得數學建模更能解決真實世界的問題。


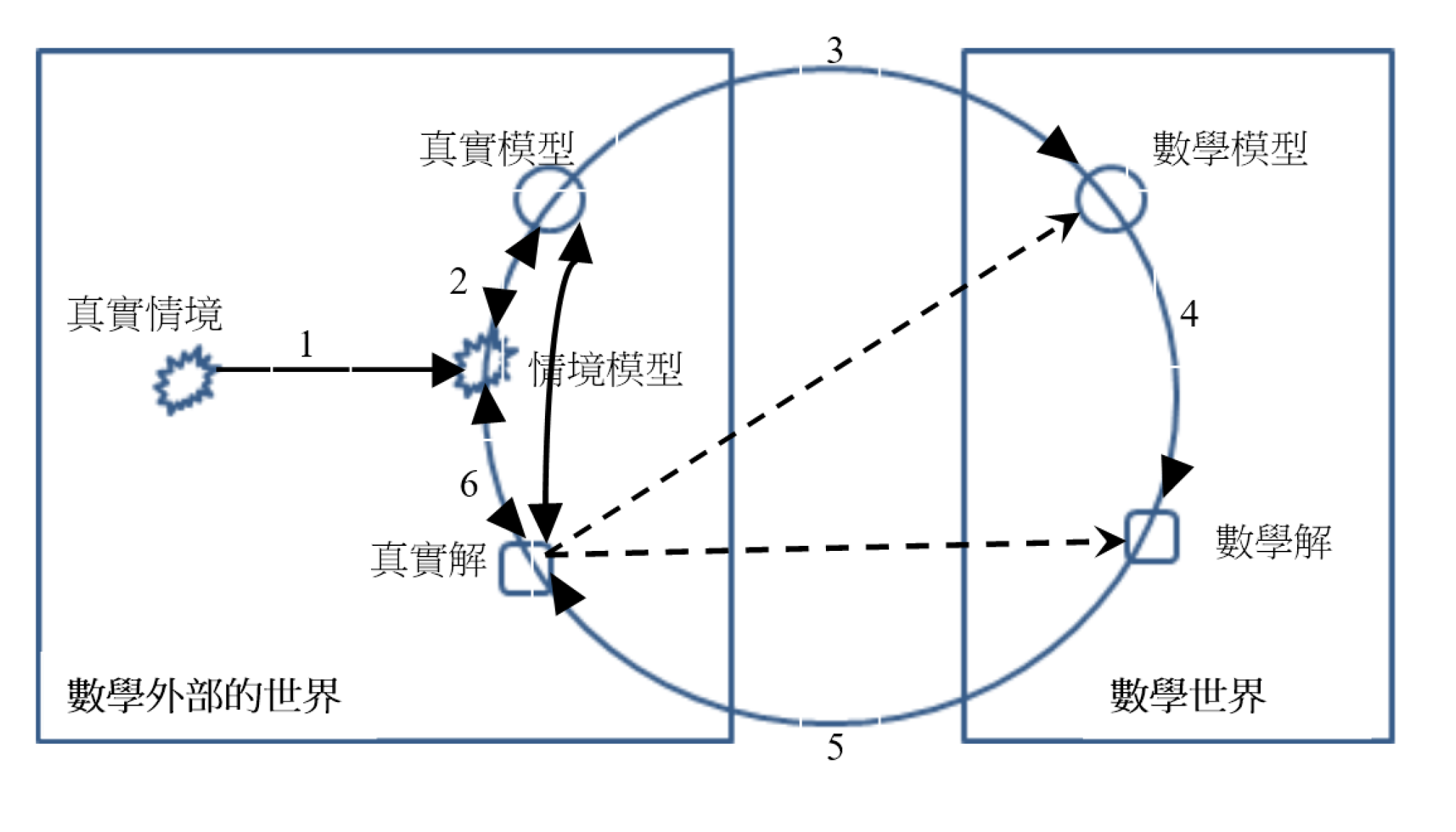圖二. The modeling cycle(修改自Blum and Leiß, 2006)

真實世界裡的「真實情境」若能以口語推論的方式找到「真實解」，這個真實解以數學語言轉成數學世界裡的「數學模型」之後有可能「無解」，亦即「口語的推論沒看到數學模型的矛盾」，因此我們在[圖二]中以虛線來表示將「真實解」轉入數學世界。以下兩節，我們以例題，來解釋[圖二]比[圖一]更能連結數學世界與真實世界！

 肆、數學建模需要豐富的生活經驗的團隊當後盾

以下題目是整合Nash, J.F. (1950) 與 Shapley L.S. (1953) 兩位諾貝爾經濟學獎得主之名著所編輯的題目，這裡我們以航空公司為主角，事實上讀者也可以用前文家庭代工合作繡花賺取工資後分錢為例。

【例題一】：假設某島國只有兩家航空公司，分別是T航空公司與C航空公司，假設這兩家航空公司不聯營，而且在市場上互相削價競爭，則T航空公司每年可賺 2 千億，C航空公司可賺 1 千億。假設T航空公司跟C航空公司聯合經營，每年可共同獲利 7 千億。問：若兩家航空公司聯合經營，他們要如何「公平」地分享這 7 千億？

假設我們看到這樣的題目，立即思考「數學外部的連結」、思考問題的「顯性數學」與「隱性數學」(李源順，2012)。然後立即給【答案1】：「對半分」；【答案2】：「按照獲利能力的比例分配」；【答案 3】：「各自先拿回原本可以獲得的利益後，餘額再按照獲利能力的比例分配」或【答案 4】：「各自先拿回原本可以獲得的利益後，餘額再對半分」。【答案1】～【答案4】的「數學內部」與「真實世界」之間的「連結」非常薄弱，在真實世界裡，航空公司往往對於【答案1】～【答案4】不會滿意！

生活經驗豐富的數學建模團隊，看到例題一的「真實情境」，不會急著遵循[圖一]的步驟，進入「數學世界」。好的數學建模團隊，會在[圖二]左邊的真實世界裡，從「真實模型」中討論出下列【答案5】與【答案6】這兩個「真實解」，再把「真實解」轉到數學世界裡的「數學模型」求「數學解」以解決真實問題。

【答案 5】（Shapley, 1953） 假設兩家航空公司，由本「數學建模團隊」來調解，如何「公平」地分配那7千億。而且經過我們的斡旋、協商兩家公司達成以下【共識】：

．共識一、分錢時與座位順序無關。以免較強勢的航空搶佔較有利的座位影響分錢的「公平」性。

．共識二、能產生邊際貢獻的公司共同把錢全部分掉；等於錢要全部分掉，而且不能產生邊際貢獻的公司無權分錢。

．共識三、上下半年兩筆帳分開算，跟上下半年合起來算各家公司所得不變。

【答案6】(Nash, 1950) 假設雙方不願意仲裁、調解。而C航空公司，找上本「數學建模團隊」來「協助」，而不是「代表」C航空公司與對方談判。並且要我們幫C航空公司設定合理的「雙贏」結果：我們會告訴C航空公司：談判的結果，至少要符合下列六個條件，C航空公司才沒有吃虧。

．條件1：談判結果比不談判好；亦即T航空公司至少必須取得比2千億以上還多，C航空公司必須取得比1千億以上還多。

．條件2：談判的最終報酬必須是雙方能力所及的(雙方所分得的金額總合不能大於7千億)。

．條件3：談判的最終報酬是無可替代的(唯一、最優)。

．條件4：在小範圍內談判有結果之後(例如：T航空公司先拿走每年可賺的2千億，C航空公司先拿走可賺的1千億，只就剩下的4千億來談，而且談出結果)，擴大範圍談判(就整個7千億談)，最終結果不是與原來小範圍內談判的結果一樣，就是最終結果在小範圍以外的區域，不會是談判結果落在原來的小區域卻與原來小區域談判的結果不同。

．條件5：用美金或用台幣計價無差別。

．條件6：若雙方的能力完全對稱，則雙方談判後的最終報酬相等。

以上【答案5】與【答案6】並非完整的解答，必須轉到數學世界做最後的數學證明與計算。其中【答案5】若更加推廣改成「多人、多種層次合作」請參考Hsiao, Chih-Ru (1991)的博士論文。本「 數學建模團隊」有將【答案6】寫成電腦程式―「談判工作表」實際應用在政府機關、企業界、產業界的談判工作。

 伍、數學建模需要具有既深且廣數學能力的團隊當後盾

一般而言，數學家在將上一節的兩個「真實解」轉到數學世界的過程中，往往會發現一些洞見(insights)。【答案5】(Shapley 1953)的三個共識，轉成數學模型求解後，「數學解」的直觀意義(intuitive meaning)是個機率分佈的期望值，計算過程中有個步驟與筆者國小五年級時發現的一個不等式不謀而合。

【不等式】：(數學內的數學建模)，觀察下面不等式：將「原式」減掉「原式每一項的分母都加1」，發現永遠會大於零。



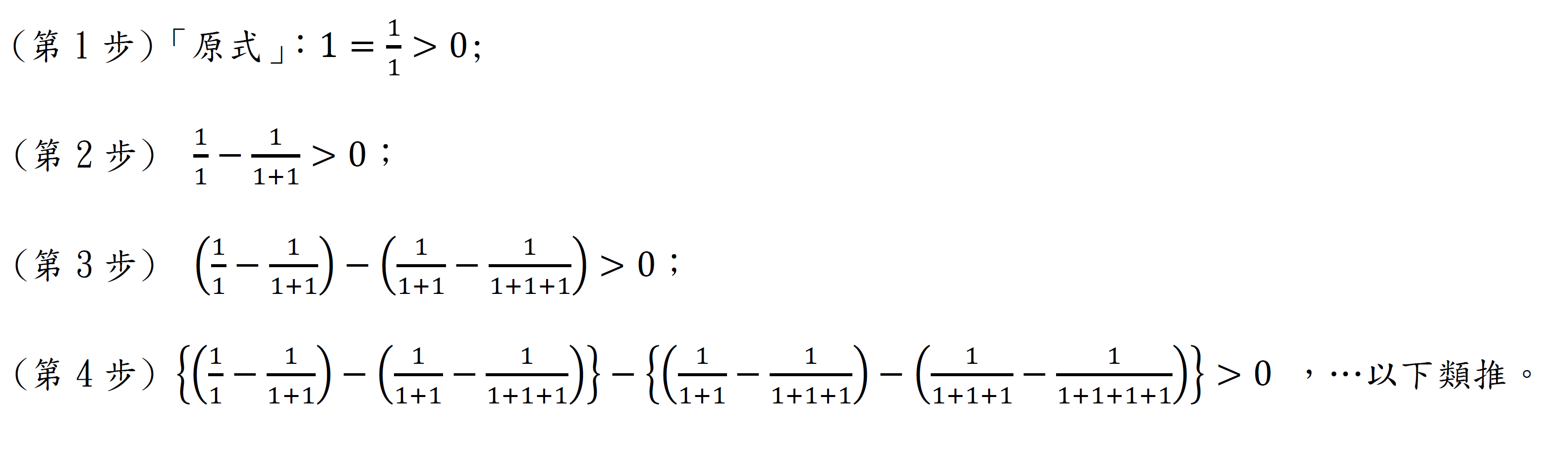
我們分別在某私立小學資優班夏令營及呂玉琴(呂玉琴、王富祥，2013)的「小數學資優生培訓營」中，帶領小學五年級的學生作上述觀察後，全部學小學生都臆測一個「數學內」的模型：「前一個式子本身，減掉前一個式子的每項分母都加1，新的數學式子嚴格大於零」。更令我們驚訝的是，在呂玉琴的「小數學資優生培訓營」中，小學生發現到我們沒發現的「第n步算出來的左式剛好等於1/n」。好的數學建模題目，不要說是數學外部的數學建模，連數學內的數學模型，小學生都能頓悟教授沒發現的。

數學家將【答案5】與【答案6】轉成數學符號後，雖然不簡單，但也不是無法將其中簡單的部份融入國小國中高中教材。上述不等式可給高中以下的學生，證明「第n步算出來的左式剛好等於1/n」的過程曾經是伊利諾大學大一微積分的習題。以下我們附上【答案5】的「共識一」之類題。

【例題二】、數學建模題；請用數學符號表現出下列敘述：有３位同學要共同分掉 100元，每位同學所得的錢與座位無關。

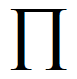
答：令１，２，３分別代表這３位同學， 為這３位同學的所有可能排列所 成的集合。



(註：【例題二】有出現在林國源(2005)的碩士論文，他的論文裡面有清楚說明這個例題是我們私下意見交流時，由蕭志如提供給他的。)

 陸、結語與建議

早在2020年元月5日，我國還沒有辦法使用「即時反轉錄聚合酶連鎖反應」（Real-Time RT-PCR）來檢驗新冠肺炎時，我國疾管署就以至少做26種病原檢驗的方式來篩檢不明新型肺炎。從數學建模的角度來看，我國疾病管制署採用的是Analysis of competing hypotheses (ACH) 這個「數理邏輯」的數學模型！數學建模的重要性不言可喻。相較於德國，我國的數學建模教育還有一段很長的路要走。雖然要使數學建模作為操作實務與建構理論的關鍵橋樑，需要很富有實務經驗又具有既深且廣的數學能力之團隊才有辦法達成任務，但是也不是完全無法融入學校教材。如果我們能夠在每一個數學單元，都附上一個完整的故事，讓學生看得到這個單元的相關應用，例如：讓學生知道上述不等式及例題一，居然是兩位諾貝爾獎得主名著論文的計算過程之一，又例如：讓學生學習機率期望值時理解處理古巴飛彈危機甚至處理1996年台海飛彈危機居然用到這些數學觀念，應該能提升學生的學習興趣。以上有賴學界各方開放胸襟跨領域合作，成立富有實際操作經驗又具有既深且廣的數學能力之數學教育研究團隊。