若問學生：「什麼是數學？」所得的答案大致上可以分為三類，一是計算數字的學科，二是需要邏輯思考的科學，三是解決問題的工具。這三類答案都只說出部份的事實。對一門已經在世界各地文明演化數千年，且與人類文化發展息息相關的學問來說，要三言兩語回答「什麼是數學？」就宛如瞎子摸象，終究只得片面真相。有次訪談一位學生問他：「什麼是數學？」，他思索片刻之後回答：「不識廬山真面目，只緣身在此山中」，真是非常傳神！即使如瞎子摸象，我們倒可以從文化的角度來理解數學知識的本質。本文所謂的「數學文化」包含「文化中的數學」和「數學中的文化」兩個構面。「文化中的數學」是指在人類發展過程中數學在社會所扮演的角色，「數學中的文化」則指數學知識發展過程中其內部所顯現的特質，這兩者呈現一種交錯的有機互動發展。本文舉兩個例子具體說明「數學文化」的概念。

 一、柏拉圖多面體

古希臘哲學思想與數學息息相關，這主要與畢達哥拉斯「萬物皆數」的理念有關。古希臘哲學重視幾何的原因在於其論證過程的嚴謹與思想上的純粹，例如正多面體就是一個例子。所謂正多面體，是指一個凸多面體之各面都是由相同的正多邊形所組成。例如我們一般所熟悉的金字塔狀的多面體並不是正多面體，因為它是由四個正三角形和一個正方形所組成，不符合正多面體的定義。由於正多面體的定義很嚴格，所以古希臘數學家好奇究竟有多少個正多面體？西元前500年左右，畢達哥拉斯學派確認了正四面體、正六面體和正十二面體。西元前399年左右，柏拉圖的朋友特埃特圖斯 (Theaetetus) 發現了正八面體和正二十面體，並告訴柏拉圖正多面體總共只有五個。柏拉圖對這五個完美對稱的立體讚嘆不已，除了將這些正多面體記載在《蒂邁歐斯》(Timaeus) 中之外，並賦與這五個正多面體具體的象徵。當時古希臘哲學家咸認「水」、「火」、「土」、「氣」是宇宙四個基本元素，柏拉圖就認為有尖銳稜角的正四面體、正八面體和正二十面體具穿透性，因此分別代表「火」、「氣」和「水」等三種元素(圖一、圖二、圖三)。而正六面體外型最安定，故代表「土」(圖四)。而剩下的正十二面體則以其較為渾圓的外觀代表「天」（或「以太」）(如圖五)。自此之後，五個正多面體被批上一層神秘的外衣，因此也被稱為柏拉圖立體。


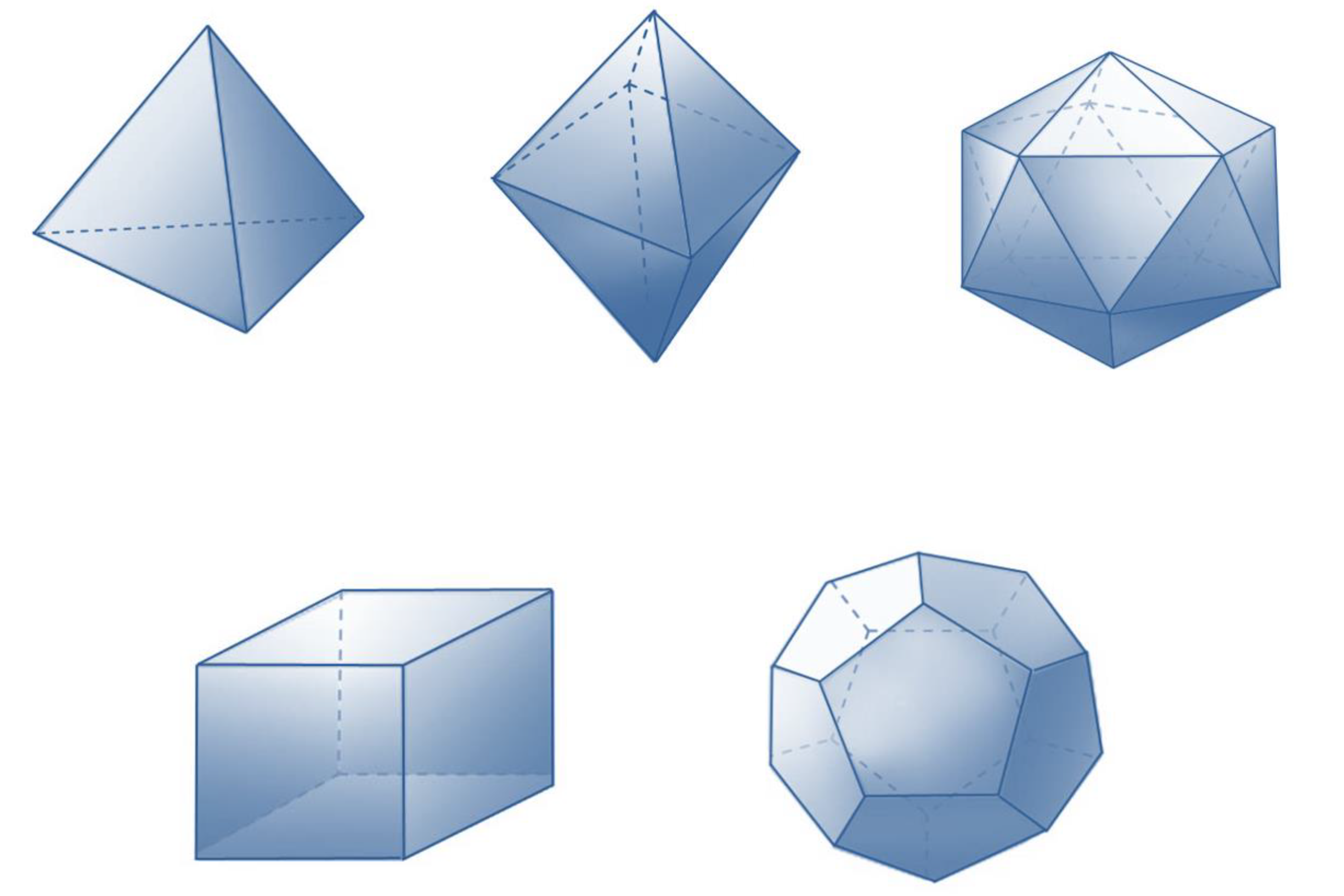圖1-5.正四面體代表火、正八面體代表氣、正二十面體代表水、正六面體代表土、正十二面體代表天

為什麼正多面體總共只有五個？柏拉圖在《蒂邁歐斯》中並沒有證明為何柏拉圖立體只有五個，難道不會出現第六個正多面體嗎？歐幾里得在《幾何原本》第十三冊中描述了建構柏拉圖立體的方法，並證明不存在其它的正多面體。不過，我們從邏輯推理上可以直覺地理解這個事實。為清楚這個事實，首先必須先確認兩件事情。第一，正多面體上的每一個頂點至少必須與三個平面互相聚接在一起，否則無法形成一封閉立體。再者，各平面中與頂點聚接的所有多邊形內角的角度總和必須小於360度，否則各平面黏接後會平鋪成一個水平面，無法形成頂點。所以對一個正三角形，由於內角均為60度，所以我們頂多只能把三個、四個和五個正三角形聚接以形成一個頂點，這樣就可以構成正四面體、正八面體和正二十面體。對正四邊形而言，由於每一內角均為90度，所以我們只可能將三個正四邊形聚接形成一個頂點，這就構成了正六面體。而正五邊形內角為108度，因此也只能聚接三個正五邊形於一點，因此得到正十二邊形。如此一來，我們就得到五個柏拉圖立體。那可不可能存在由正六邊形所組成的正多面體呢？這是不可能的，因為正六邊形的內角為120度，而三個角聚接於一點將形成360度，構成一平面，不可能組合成立體。接下來，邊數大於六邊的正多邊形其內角均大於120度，更不可能構成正多面體。

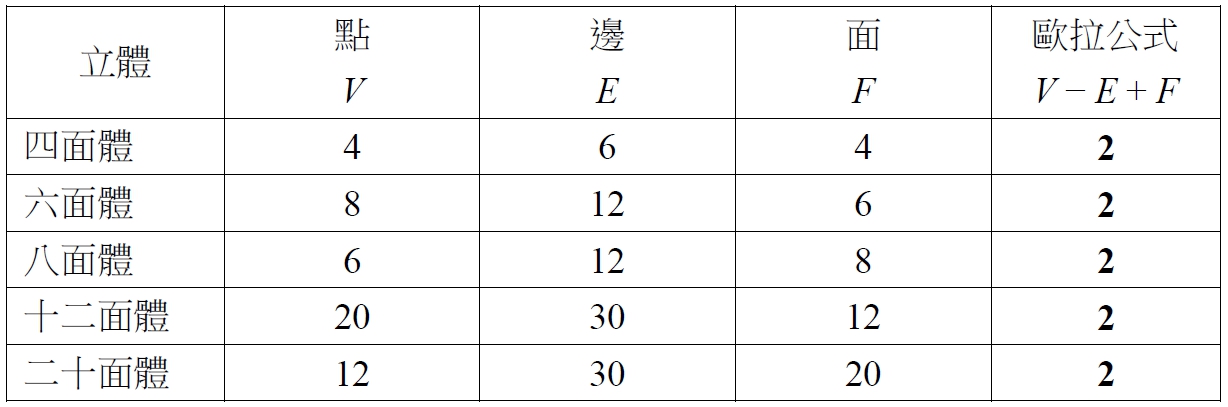
柏拉圖立體的性質很明顯是從古希臘的哲學文化中所產生的數學問題，屬於「文化中的數學」。不過一個問題一旦與「數」和「形」扯上關係，就會吸引數學家的注意。例如十八世紀瑞士數學家歐拉開始關心多面體之「點」、「邊」和「面」個數之間的關係。這個問題很適合做為讓學生發現數學規律的建構活動，透過教具操作和觀察(圖6)，學生不難發現其規律(見表1)，也就是正多面體的頂點的個數V加上面的個數F一定比邊的個數E多2(即V − E + F=2)。


圖6.學生創作多面體

表1.正多面體之點邊面個數的關係


只是這規律對所有的多面體都成立嗎？這問題可以引導學生嘗試將特殊性質一般化，是「數學中的文化」的典型思維模式。此時讓學生繼續探究，他們可能會逐漸體認到上述規律對一般的多面體都成立，惟當他們做出如圖7的星狀多面體時，會突然發現這個規律被打破了！圖七的星狀多面體是一個凹多面體，原來V − E + F=2這規律只對所有的凸多面體成立。至於凹多面體的規律就相當分歧，無法一言以蔽之。拉卡托斯(Imre Lakatos)在《證明與反駁》一書中就利用臆測與論證探討各式多面體中點、邊、面個數的關係，充分展現「數學中的文化」如何琢磨一個數學概念。如今多面體中點、邊、面個數的關係被稱為「歐拉特徵數」(Euler characteristic，又稱歐拉示性數)，是代數拓樸中的一個研究主題。


圖7.星狀凹多面體

 二、七橋問題

《周易．繫辭上》：「河出圖，洛出書，聖人則之。」所講的是兩個中國古代神話，其一是伏羲氏見龍馬背河圖(圖8) 感悟出自然變化的規律。河圖中的「天數」(就是奇數，以白點表示)是1、3、5、7、9，總和為25，「地數」(就是偶數，以黑點表示)是2、4、6、8、10，總和為30，所以河圖的天地數為55，且「天數」與「地數」具有一些配對法則。其二是大禹遇神龜負洛書(圖9)領略出治理天下的道理，其「天數」是1、3、5、7、9，總和為25，「地數」是2、4、6、8，總和為20，所以洛書的天地數為45，其縱橫斜排數字之和都是15，而河圖和洛書的天地數相加恰好等於100。這說明數學在人類的歷史發展中，最初的功能就是用於解決日常實際問題。


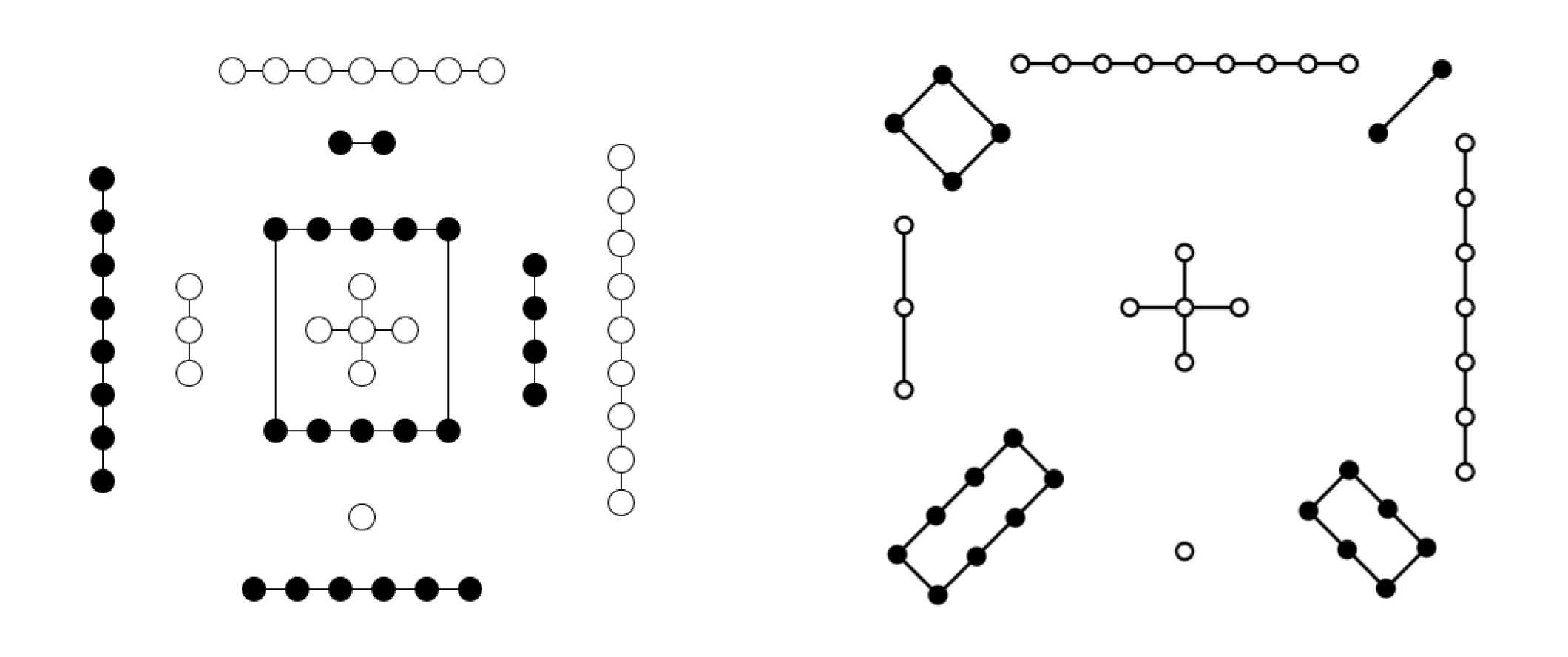圖8.河圖（左）圖9.洛書（右）（圖片來源：維基百科）

知名的哥尼斯堡七橋問題的出現也反映「文化中的數學」之內涵。哥尼斯堡就是現今俄羅斯加里寧格勒州的首府加里寧格勒(Kaliningrad)，圖10是哥尼斯堡十七世紀時的市區地圖，其中普列哥利亞河流經市區，哥尼斯堡大教堂所在的陸地被河水環繞，與四邊的陸地依靠七座橋聯結。市民想知道可不可能一次走完七座橋經過這四塊區域，且每座橋只能經過一次？這時歐拉又登場了。當歐拉知道之後便開始著手思考這問題，最後證明符合這種條件的走法並不存在，並向聖彼得堡科學院提出論文。歐拉採取邏輯推論的方式論證七橋問題的不可能性。推論過程可以分為「符號化」、「問題重述」、「啟發式分析」和「豁然開朗」四個階段。


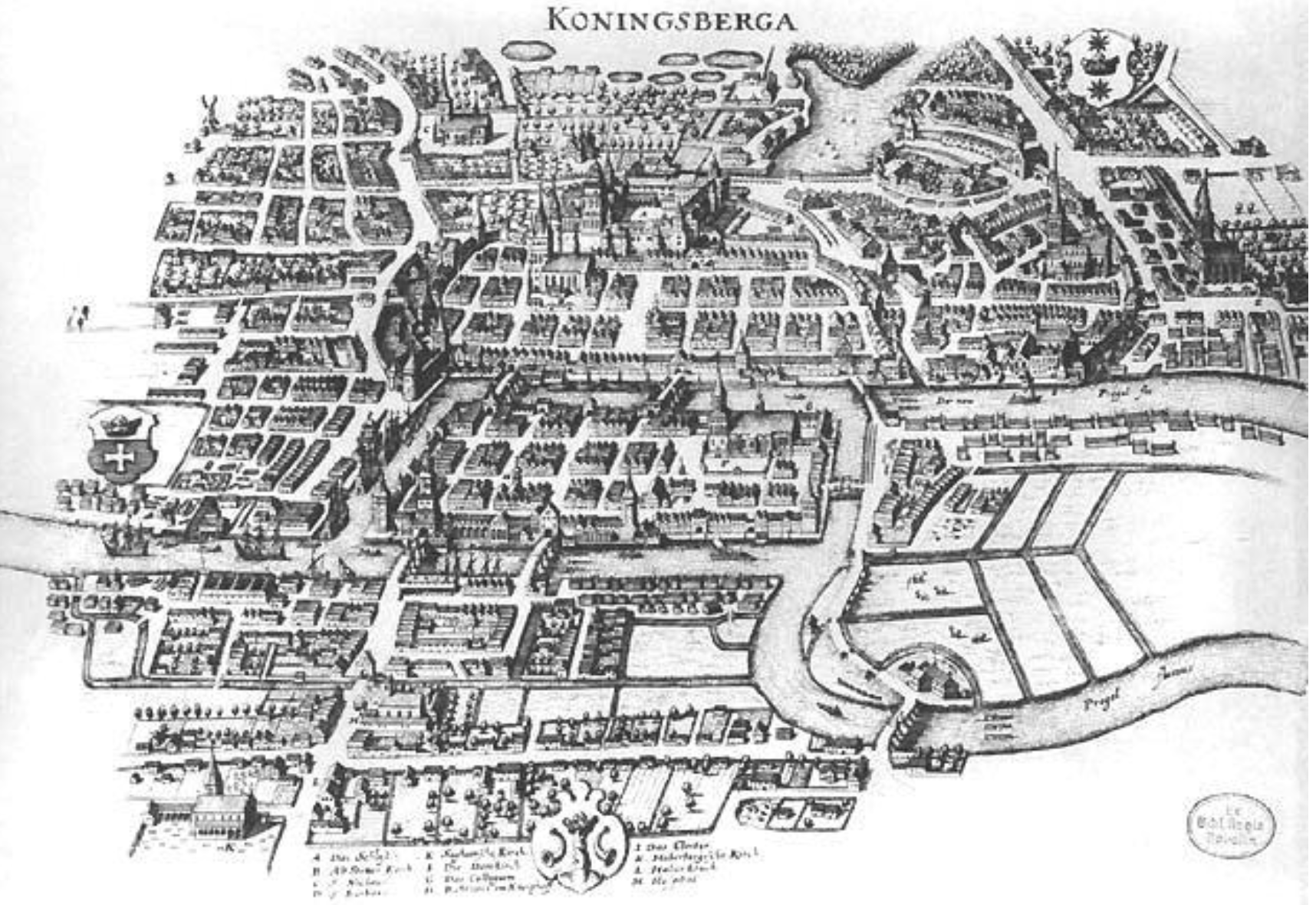圖10.十八世紀哥尼斯堡市區地圖（圖片來源：維基百科）

一、符號化
如圖11，歐拉用大寫字母A, B, C, D分別表示被普列哥利亞河分開的四塊陸地，小寫字母a, b, c, d, e, f, g表示七座橋。當一個人從A地走到B地，無論是經過橋a(AaB)或橋b(AbB)，歐拉都記作“AB”。如果接著從B又回到A，則記為ABA。同理，如果是緊接著從B過橋 f 到D，記作ABD。

二、問題重述
按照歐拉的記法，記錄過橋次數的字串中，代表陸地的字母個數一定比橋的個數多一個。因此，如果七座橋各僅通過一次，則七橋問題可以重新敘述為：「走過七座橋的路徑有沒有可能用A,B,C,D四個字母所組成的八個字母表示？」


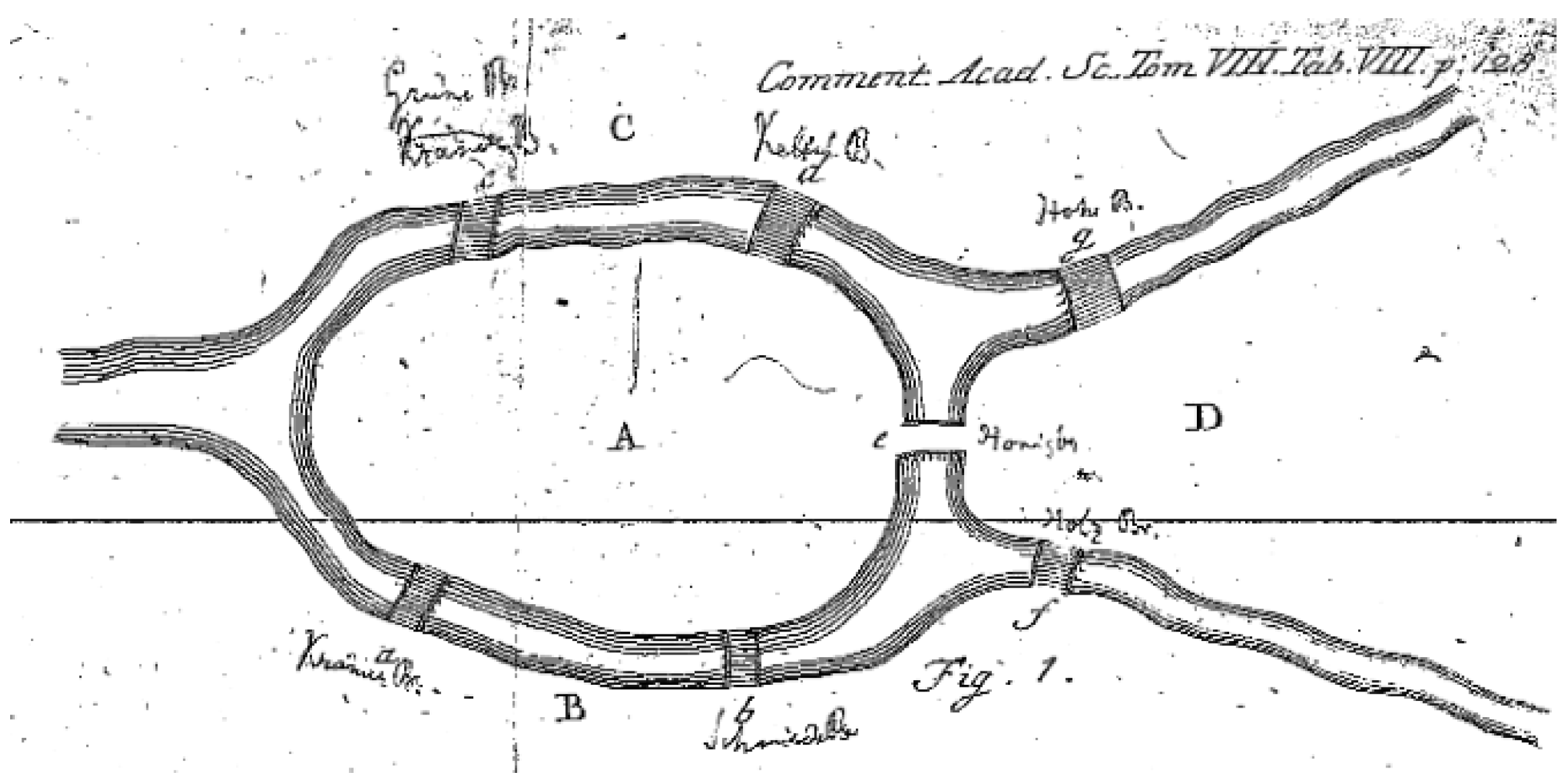
圖11.歐拉論文中的哥尼斯堡地圖

三、啟發式分析
歐拉接著觀察簡化後的圖12，他發現如果A和B只有一座橋a相連，不論是A走到B還是B走到A，A一定只出現一次(AB或BA)。如果A和B三座橋 a, b, c, 連接，那麼不管是不是從 A出發，A都將出現兩次(即ABAB或BABA)。如果A和五座橋a,b,c,d,e相連，則A出現三次。依此類推，如果與A連接的橋數k是奇數，則A出現的次數為 (k + 1)/2。


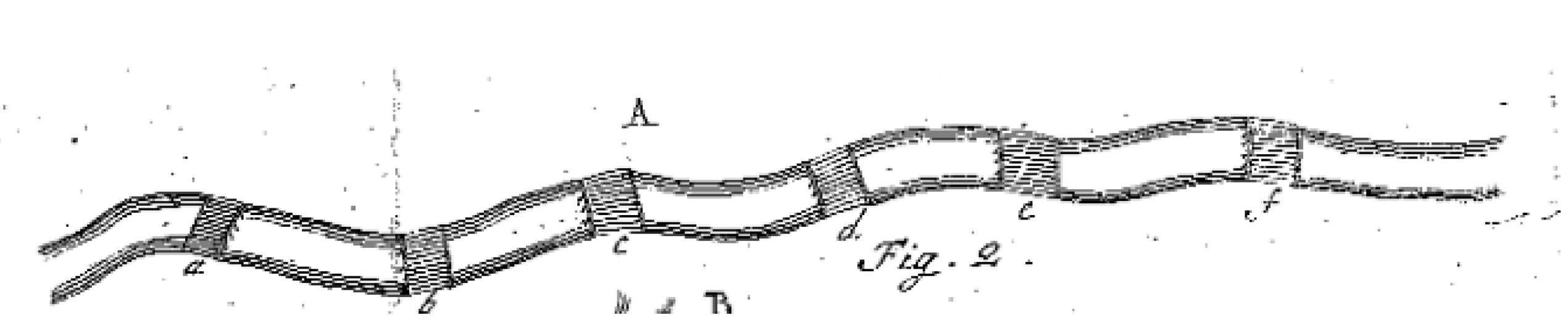
圖12.英文字母數與橋數的關係

四、豁然開朗
回到七橋問題本身。根據前述分析，由於連接A的有5座橋，所以在字串中A應出現3次，連接B, C, D的各有3座橋，因此它們各出現2次，這樣如果七座橋各走過一遍，字串中總字母的個數應該等於 3+2+2+2 = 9，但我們前面已說過，走過七座橋僅需要八個字母的字串，彼此相互矛盾，因而七橋問題無解。
「七橋問題」是「數學文化」一個典型的案例。它很明顯是從文化中所衍生出的數學。歐拉解決七橋問題的過程中充分展現數學素養，也就是面臨一個真實生活的問題時能辨識它與數學的關聯，從而根據數學知識和適當工具去描述、模擬、解釋與預測各種現象，發揮數學思維方式的特長，做出理性反思與判斷。不過雖然歐拉透過「問題符號化-問題重述-啟發式分析-豁然開朗」的推理過程展現他的思路歷程，卻沒有給予嚴格的證明，這很可能是因為當時的他認為哥尼斯堡問題與數學關係甚少，解答過程只靠推理，沒根據任何數學性質，所以不需要證明。雖然在解析幾何當道的那個年代這觀點合理，但是一旦問題被符號化，就進入「數學中的文化」所管轄的領域。隨後哥尼斯堡地圖被簡化為圖13的模樣，「陸地」變成「點」，「橋梁」變成「線」，A點與5個邊相連，B,C,D各與3個邊相連，能不能一次走過七座橋，變成「一筆畫遊戲」的休閒問題，與各點相連邊數的奇偶數有關。當圖形被抽象化，各個點被賦予數值權重後，七橋問題隨之轉化為圖形理論的基礎，其後又進化成拓樸學，這就是「數學文化」的歷程。


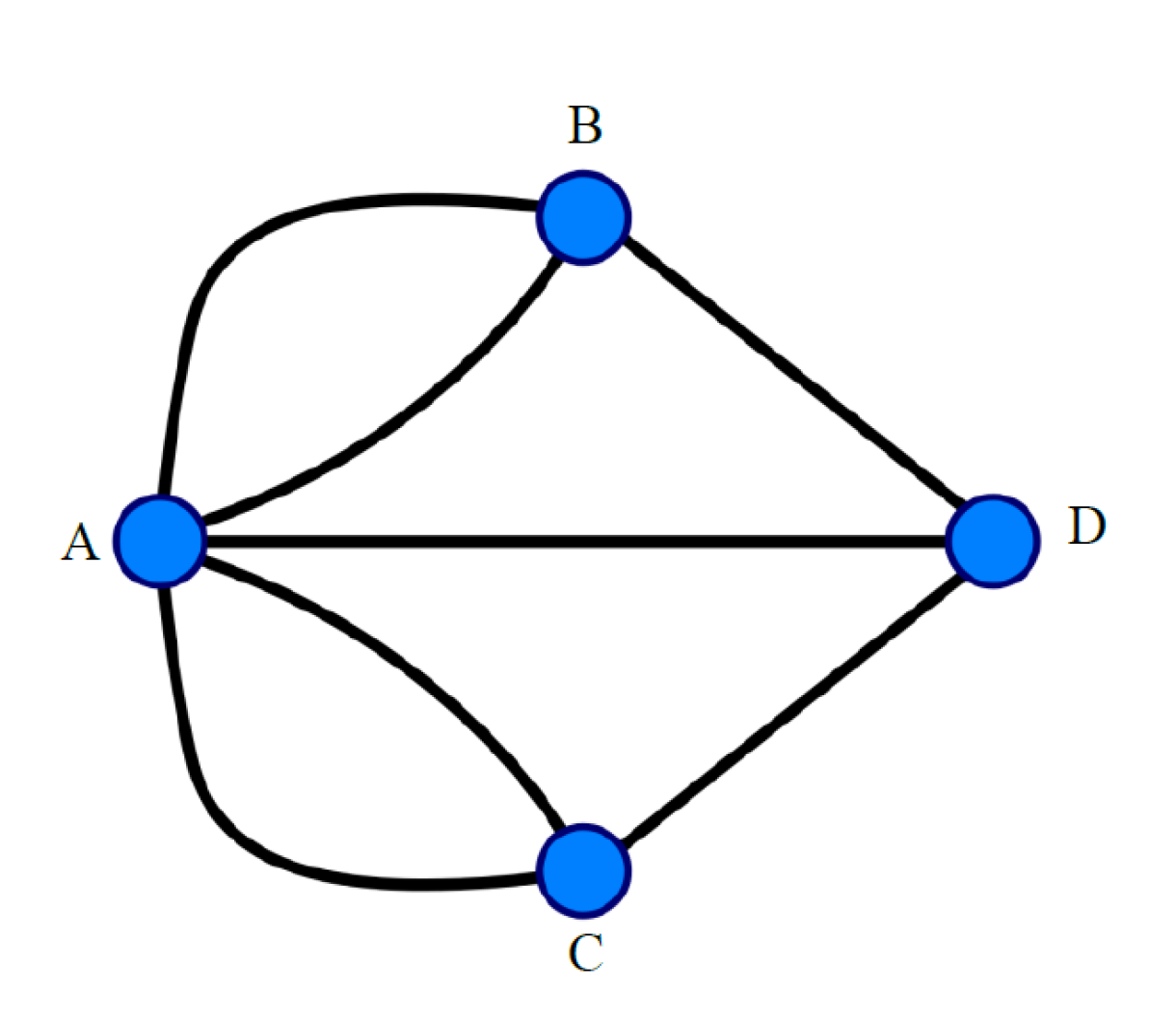
圖13.七橋問題抽象圖（圖片來源：維基百科）

 三、數學文化素養

108課綱強調數學素養，但是數學素養一詞範圍廣泛，它的涵義不容易精準掌握。透過數學文化，可以認識數學本質，而認識數學本質就是增進數學文化素養。依據數學素養的定義，我們可以將數學文化素養定義如下：

數學文化素養係指個體對數學知識的形成脈絡和發展過程所具備的理解程度，使其面對某一數學概念或問題時，能認識它的思維方式、歷史背景，和該概念或問題與生活需求、社會發展的關聯；或是面臨生活與社會問題時，能辨識該問題與數學知識的關聯，從而根據數學思考模式和數學知識技能，做出理性反思與判斷，並從解決問題的歷程中認知數學的人文價值。

本文所舉的兩個案例都是從「文化中的數學」出發，然後遵循「數學中的文化」發展成數學知識的一環，而這些數學知識又進一步影響其他領域，形塑成另一種文化。例如柏拉圖立體由於其對稱之美和柏拉圖所賦與的神性，使得後世數學家和藝術家一直持續關注，也對科學和藝術發生諸多影響。十六世紀天文學家克卜勒 (Johannes Kepler)曾建構一個以柏拉圖立體為基礎的太陽系模型。二十世紀荷蘭藝術家艾雪 (Maurits Cornelis Escher)著迷於柏拉圖立體，乃至於其他多面體的幾何之美。數學文化素養所訴求的就是，除了能理解問題背後的數學性質的同時，也能認識這些問題在我們人類文化中所代表的意涵。