大家都知道,二條平行線之間處處等距離,那麼同學有沒有想過,既然處處等距離,這個距離有沒有什麼方法可以算出來?請看底下二個例題的說明:
例一:設直線L1:3x+4y=12 , L2:3x+4y=24 ,試求L1 和L2 的距離?
解:
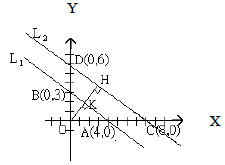
L1:
A(4,0),B(0,3)
則 AB =  = 5 = 5
L2:
C(8,0), D(0,6)
則 CD = 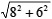 = 10 = 10
作 OH ⊥ CD 於H 並交 AB 於K ,則 OH 為直角三角形OCD斜邊上的高, OK 為直角三角形OAB斜邊上的高。
因此
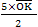 = △OAB面積 = = △OAB面積 = 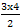 → OK = → OK = 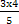 = = 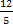
同理
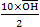 = △OCD面積 = = △OCD面積 = 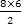 → OH = → OH = 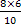 = = 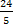
故此二平行線之間的距離為
KH = OH - OK = 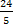 - - 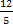 = = 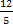
例二:設直線L1:4x+3y=12 ,L2:4x+3y=-24 ,試求L1 和L2 的距離?
解:
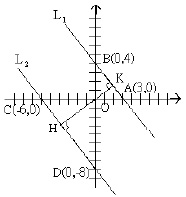
L1:
A(3,0),B(0,4)
則 AB =  = 5 = 5
L2:
C(-6,0), D(0,-8)
則 CD = 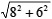 = 10 = 10
作 OH ⊥ CD 於H 並延長 OH 交 AB 於K ,則 OH 為直角三角形OCD斜邊上的高, OK 為直角三角形OAB斜邊上的高。
因此
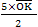 = △OAB面積 = = △OAB面積 = 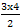 → OK = → OK = 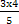 = = 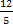
同理
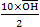 = △OCD面積 = = △OCD面積 = 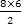 → OH = → OH = 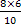 = = 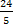
故此二平行線之間的距離為
KH = OH + OK = 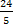 + + 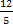 = = 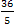
從上面兩個例子可以看出,有關於二條平行線之間的距離的問題可以利用直角三角形斜邊上的高的技巧予以算出,接下來再看一般的型式。
對於一般的二條平行線L1:a1x+b1y=c1 和L2:a1x+b1y=c2 ,其中c1 ≠ c2 (因為任意二條平行線的方程式,其x 項係數和y 項係數成某一比例關係,故可以假設成一樣的係數。)
L1:
| X |
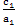 |
0 |
| Y |
0 |
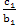 |
A(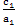 ,0), B( 0 , ,0), B( 0 ,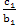 ) )
則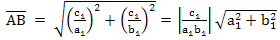
設 OK 為直角三角形OAB斜邊上的高
因 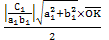 = △OAB面積 = = △OAB面積 = 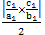
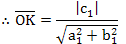
L2:
| X |
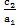 |
0 |
| Y |
0 |
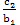 |
A(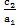 ,0), B( 0 , ,0), B( 0 ,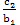 ) )
則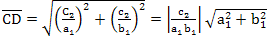
設 OH 為直角三角形OCD斜邊上的高
因 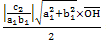 = △OCD面積 = = △OCD面積 = 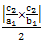
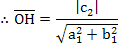
(1)若c1c2 > 0 (即c1 和c2 同號) 表示 OK 和 OH 會有一部份重合在一起(如例一:12 和24 同號,因此 OK 是 OH 的一部份)
因此
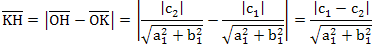 (註1) (註1)
(2)若c1c2 < 0 (即c1 和c2 異號) 表示 OK 和 OH 方向不一樣,不會有重合的情況(如例二:12 和-24 異號,因此 OK 和 OH 不會有重合的情況)
因此
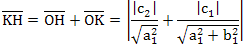 (註2) (註2)
由上述二種討論,我們可知兩平行線之間的距離為 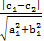
實例驗證
我們再驗證例一和例二。
例一的驗證:
a1 = 3 , b1 = 4 , c1 = 12 , c2 = 24
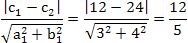
例二的驗證:
a1 = 4 , b1 = 3 , c1 = 12 , c2 = 24
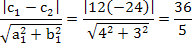
與前面的計算相吻合。
|